Phương pháp giải:

- Chứng minh \(SH \bot \left( {ABC} \right)\).

- Gọi M, N lần lượt là trung điểm của BC, MC. Chứng minh \(BC \bot \left( {SHN} \right)\).

- Trong (SHN) kẻ , chứng minh \(HK = {d_{\left[ {H;\left( {SBC} \right)} \right]}}\).

- Sử dụng tỉ số lượng giác của góc nhọn, định lí Pytago, hệ thức lượng trong tam giác vuông để tính HK.

Lời giải chi tiết:

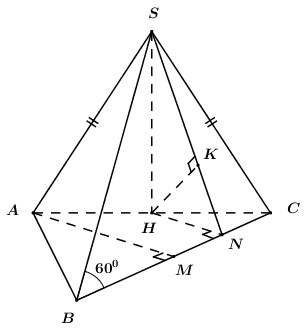
+ \(\Delta SAC\) cân tại S \( \Rightarrow SH \bot AC\).

+ \(\left\{ \begin{array}{l}\left( {SAC} \right) \bot \left( {ABC} \right) = AC\\SH \subset \left( {SAC} \right);\,\,SH \bot AC\end{array} \right.\) \( \Rightarrow SH \bot \left( {ABC} \right)\).

Gọi M, N lần lượt là trung điểm của BC, MC.

+  đều \( \Rightarrow AM \bot BC\) , HN là đường trung bình của tam giác ACM \( \Rightarrow HN\parallel AM\).

\( \Rightarrow HN \bot BC\).

+ \(\left\{ \begin{array}{l}BC \bot HN\\BC \bot SH\end{array} \right. \Rightarrow BC \bot \left( {SHN} \right)\).

Trong (SHN) kẻ \(HK \bot SN\) \(\left( {K \in SN} \right)\).

+ \(\left\{ \begin{array}{l}HK \bot SN\\HK \bot BC\,\,\left( {BC \bot \left( {SHN} \right)} \right)\end{array} \right. \Rightarrow HK \bot \left( {SBC} \right)\).

\( \Rightarrow {d_{\left[ {H;\left( {SBC} \right)} \right]}} = HK\).

+ \(\Delta ABC\) đều cạnh a \( \Rightarrow AM = \dfrac{{a\sqrt 3 }}{2}\) \( \Rightarrow HN = \dfrac{{a\sqrt 3 }}{4}\).

+ : \(BN = \dfrac{3}{4}BC = \dfrac{{3a}}{4}\) \( \Rightarrow SN = BN.\tan {60^0} = \dfrac{{3a\sqrt 3 }}{4}\).

+ \(\Delta SHN\): \(SH = \sqrt {S{N^2} - H{N^2}}  = \sqrt {\dfrac{{27{a^2}}}{{16}} - \dfrac{{3{a^2}}}{{16}}}  = \dfrac{{a\sqrt 6 }}{2}\).

    \(HK = \dfrac{{SH.HN}}{{\sqrt {S{H^2} + H{N^2}} }} = \dfrac{{\dfrac{{a\sqrt 6 }}{2}.\dfrac{{a\sqrt 3 }}{4}}}{{\sqrt {\dfrac{{3{a^2}}}{2} + \dfrac{{3{a^2}}}{{16}}} }} = \dfrac{{a\sqrt 6 }}{6}\).

Vậy \({d_{\left[ {H;\left( {SBC} \right)} \right]}} = \dfrac{{a\sqrt 6 }}{6}\).