Câu hỏi
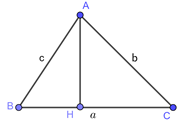
Cho tam giác \(ABC\) có góc \(B\) nhọn, các cạnh \(BC = a;AC = b;AB = c\).
Chứng minh rằng: \({S_{ABC}} = \frac{1}{2}ac\sin B\).
Phương pháp giải:
Sử dụng định nghĩa tỉ số lượng giác.
Công thức tính diện tích tam giác.
Lời giải chi tiết:
Xét \(\Delta ABH\)vuông tại \(H\) có:
\(sinB = \frac{{AH}}{{AB}} \Leftrightarrow sinB = \frac{{AH}}{c} \Leftrightarrow AH = csinB\)
\({S_{ABC}} = \frac{{AH.BC}}{2} = \frac{1}{2}ac\sin B\) (đpcm)
Câu hỏi trước
