Câu hỏi
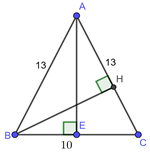
Cho tam giác \(ABC\) cân tại \(A\) có \(AB = AC = 13cm\); \(BC = 10cm\). Tính \(sinA\).
- A \(\sin A = \frac{{120}}{{169}}\)
- B \(\sin A = \frac{{60}}{{169}}\)
- C \(\sin A = \frac{5}{6}\)
- D \(\sin A = \frac{{10}}{{13}}\)
Phương pháp giải:
Sử dụng định nghĩa tỉ số lượng giác
Tính chất tam giác cân.
Công thức tính diện tích tam giác
Lời giải chi tiết:
Vì tam giác \(ABC\) cân tại\(A\) nên là \(AE\) đường cao đồng thời là đường trung tuyến
\( \Rightarrow E\) là trung điểm \(BC \Rightarrow EB = EC = 5\)
Xét \(\Delta ABE\)vuông tại \(E\) có:
\(A{E^2} + E{B^2} = A{B^2}\) (Định lý Pi-ta-go)
\(A{E^2} + {5^2} = {13^2} \Rightarrow AE = 12\)
\( \Rightarrow {S_{ABC}} = \frac{{AE.BC}}{2} = \frac{{12.10}}{2} = 60\)
Mặt khác: \({S_{ABC}} = \frac{{AC.BH}}{2} \Leftrightarrow 60 = \frac{{13.BH}}{2}\)\( \Rightarrow BH = \frac{{120}}{{13}}\)
Xét \(\Delta ABH\)vuông tại \(H\) có: \(sinA = \frac{{BH}}{{BA}} = \frac{{120}}{{13}}:13 = \frac{{120}}{{169}}.\)
Chọn A.