Câu hỏi
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AD = 2a. Cạnh bên SA vuông góc với đáy, SA = 2a. Khoảng cách giữa hai đường thẳng AB và SD bằng:
- A \(a\sqrt 2 \)
- B \(\dfrac{{2a}}{{\sqrt 5 }}\)
- C \(2a\)
- D \(a\)
Phương pháp giải:
- Sử dụng định lí: Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa đường thứ nhất đến mặt phẳng song song với nó và chứa đường thứ hai.
- Quy về bài toán tính khoảng cách từ chân đường vuông góc đến mặt phẳng.
- Dựng khoảng cách, sử dụng tính chất tam giác vuông cân hoặc hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
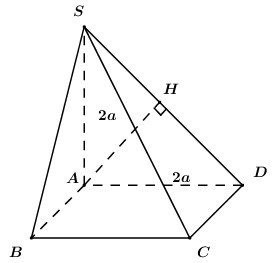
Ta có: \(AB\parallel CD\,\,\left( {gt} \right) \Rightarrow AB\parallel \left( {SCD} \right) \supset SD\).
\( \Rightarrow d\left( {AB;SD} \right) = d\left( {AB;\left( {SCD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right)\).
Trong (SAD) kẻ \(AH \bot SD\,\,\left( {H \in SD} \right)\) ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot AH\\\left\{ \begin{array}{l}AH \bot SD\\AH \bot CD\end{array} \right. \Rightarrow AH \bot \left( {SCD} \right)\\ \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = AH\\ \Rightarrow d\left( {AB;SD} \right) = AH\end{array}\)
Vì tam giác SAD vuông cân tại A có \(SA = AD = 2a \Rightarrow AH = \dfrac{{SA}}{{\sqrt 2 }} = a\sqrt 2 \).
Vậy \(d\left( {AB;SD} \right) = a\sqrt 2 \).
Chọn A.







