Lời giải chi tiết:

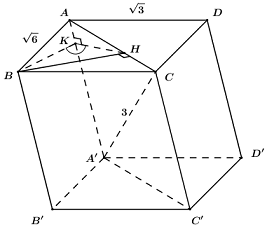
Trong (ABCD) kẻ \(BH \bot AC\,\,\left( {H \in AC} \right)\), ta có:

\(\left\{ \begin{array}{l}\left( {ABCD} \right) \bot \left( {ACC'A'} \right) = AC\\AH \subset \left( {ABCD} \right),\,\,AH \bot AC\end{array} \right.\) \( \Rightarrow AH \bot \left( {ACC'A'} \right)\).

Trong (ACC’A’) kẻ \(HK \bot AA'\,\,\left( {K \in AA'} \right)\) ta có: \(\left\{ \begin{array}{l}HK \bot AA'\\BH \bot AA'\end{array} \right.\) \(AA' \bot \left( {BHK} \right) \Rightarrow AA' \bot BK\).

\(\left\{ \begin{array}{l}\left( {ACC'A'} \right) \cap \left( {AA'B'B} \right) = AA'\\HK \subset \left( {ACC'A'} \right);\,\,HK \bot AA'\\BK \subset \left( {ACC'A'} \right);\,\,BK \bot AA'\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {ACC'A'} \right);\left( {AA'B'B} \right)} \right) = \angle \left( {HK;BK} \right) = \angle BKH = \alpha \).

Ta có: \(BH \bot \left( {ACC'A'} \right) \Rightarrow BH \bot HK\) \( \Rightarrow \Delta BHK\) vuông tại H.

Ta có: \(BH = \dfrac{{AB.BC}}{{\sqrt {A{B^2} + B{C^2}} }} = \dfrac{{\sqrt 6 .\sqrt 3 }}{{\sqrt {6 + 3} }} = \sqrt 2 \).

\( \Rightarrow HK = BH.\cot \alpha  = \sqrt 2 .\dfrac{4}{3} = \dfrac{{4\sqrt 2 }}{3}\).

Áp dụng hệ thức lượng trong tam giác vuông ABC ta có: \(AH = \dfrac{{A{B^2}}}{{AC}} = \dfrac{6}{{\sqrt {6 + 3} }} = 2\).

Xét tam giác vuông AHK có: \(\sin \widehat {HAK} = \dfrac{{HK}}{{AH}} = \dfrac{{4\sqrt 2 }}{3}:2 = \dfrac{{2\sqrt 2 }}{3}\) \( \Rightarrow \cos \widehat {HAK} =  \pm \sqrt {1 - {{\sin }^2}\widehat {HAK}}  =  \pm \dfrac{1}{3} = \cos \widehat {A'AC}\)

Áp dụng định lí Cosin trong tam giác AA’C có:

TH1: \(\cos \widehat {A'AC} = \dfrac{1}{3}\)

\(\begin{array}{l}\cos \widehat {A'AC} = \dfrac{{AA{'^2} + A{C^2} - A'{C^2}}}{{2AA'.AC}}\\ \Rightarrow \dfrac{1}{3} = \dfrac{{AA{'^2} + 9 - 9}}{{2.AA'.3}}\\ \Rightarrow \dfrac{1}{3} = \dfrac{{AA'}}{6} \Leftrightarrow AA' = 2\end{array}\)

TH2: \(\cos \widehat {A'AC} =  - \dfrac{1}{3}\)

\(\begin{array}{l}\cos \widehat {A'AC} = \dfrac{{AA{'^2} + A{C^2} - A'{C^2}}}{{2AA'.AC}}\\ \Rightarrow  - \dfrac{1}{3} = \dfrac{{AA{'^2} + 9 - 9}}{{2.AA'.3}}\\ \Rightarrow  - \dfrac{1}{3} = \dfrac{{AA'}}{6}\,\,\left( {ktm} \right)\end{array}\)

\(\begin{array}{l} \Rightarrow {S_{\Delta AA'C}} = \dfrac{1}{2}AA'.AC.\sin \widehat {A'AC}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}.2.3.\dfrac{{2\sqrt 2 }}{3} = 2\sqrt 2 \\ \Rightarrow {S_{ACC'A'}} = 2{S_{\Delta AA'C}} = 4\sqrt 2 \\ \Rightarrow {V_{B.ACC'A'}} = \dfrac{1}{3}BH.{S_{ACC'A'}} = \dfrac{1}{3}.\sqrt 2 .4\sqrt 2  = \dfrac{8}{3}\\ \Rightarrow {V_{ABC.A'B'C'}} = \dfrac{3}{2}{V_{B.ACC'A'}} = 4\\ \Rightarrow {V_{ABCD.A'B'C'D'}} = 2{V_{ABC.A'B'C'}} = 8.\end{array}\) 

Chọn C.