Phương pháp giải:

+ Sử dụng biểu thức tính thế năng

+ Vận dụng trục thời gian suy ra từ vòng tròn lượng giác

Lời giải chi tiết:

Con lắc lò xo dao động theo phương ngang, ta có:

+ Thế năng: \({{\rm{W}}_t} = \dfrac{1}{2}k{x^2}\)

+ Thế năng đàn hồi cực đại: \({{\rm{W}}_{tmax}} = \dfrac{1}{2}k{A^2}\)

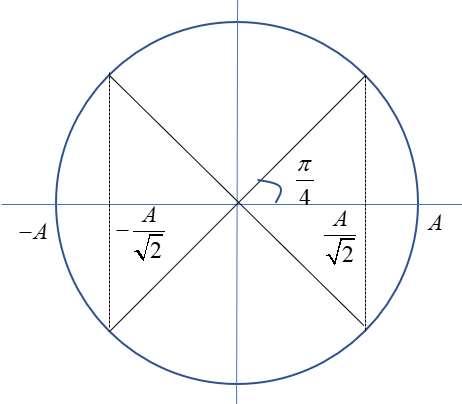
\({{\rm{W}}_t} = \dfrac{1}{2}{{\rm{W}}_{tmax}} \Leftrightarrow x =  \pm \dfrac{A}{{\sqrt 2 }}\)

Khoảng thời gian ngắn nhất giữa 2 lần thế năng đàn hồi của lò xo bằng nửa thế năng đàn hồi cực đại:

\(\Delta t = \dfrac{T}{4} = 0,15s \Rightarrow T = 0,6s\)

Chọn D