Câu hỏi
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, \(SA \bot \left( {ABCD} \right)\). Mặt phẳng qua A và vuông góc với SC cắt SB, SC, SD theo thứ tự tại H, M, K. Chọn khẳng định sai trong các khẳng định sau:
- A \(AK \bot HK\)
- B \(HK \bot AM\)
- C \(BD \bot HK\)
- D \(AH \bot SB\)
Phương pháp giải:
Sử dụng các định lí: \(\left\{ \begin{array}{l}a \bot b\\a \bot c\\b \cap b \subset \left( P \right)\end{array} \right. \Rightarrow a \bot \left( P \right)\), \(\left\{ \begin{array}{l}a \bot \left( P \right)\\d \subset \left( P \right)\end{array} \right. \Rightarrow a \bot d\).
Lời giải chi tiết:
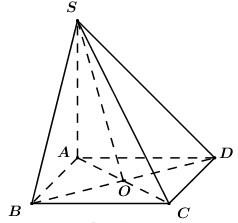
+ \(\left\{ \begin{array}{l}BC \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot AM\).
+ Gọi \(O = AC \cap BD,\,\,I = SO \cap HK\).
(P) đi qua A và vuông góc với SC. Qua I kẻ \(\Delta \parallel BD \Rightarrow \Delta \bot AM \Rightarrow \Delta \subset \left( P \right)\).
Khi đó \(K = \cap SD,\,\,H = \Delta \cap SB\).
+ \(AK \bot \left( {SCD} \right),\,\,HK \cap \left( {SCD} \right) = K \Rightarrow AK\)
+ \(\left\{ \begin{array}{l}AC \bot BD\\AC \bot SO\end{array} \right. \Rightarrow AC \bot \left( {SBD} \right)\).
Chọn C.







