Câu hỏi
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\). Gọi H, K lần lượt la trực tâm các tam giác SBC và ABC. Mệnh đề nào sai trong các mệnh đề sau?
- A \(BC \bot \left( {SAH} \right)\)
- B \(HK \bot \left( {SBC} \right)\)
- C \(BC \bot \left( {SAB} \right)\)
- D SH, AK và BC đồng quy
Phương pháp giải:
Sử dụng các định lí: \(\left\{ \begin{array}{l}a \bot b\\a \bot c\\b \cap b \subset \left( P \right)\end{array} \right. \Rightarrow a \bot \left( P \right)\), \(\left\{ \begin{array}{l}a \bot \left( P \right)\\d \subset \left( P \right)\end{array} \right. \Rightarrow a \bot d\).
Lời giải chi tiết:
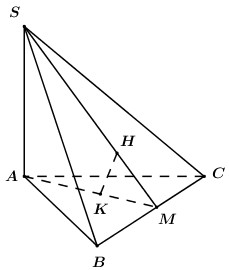
+ \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot SH\end{array} \right. \Rightarrow BC \bot \left( {SAH} \right)\). Suy ra đáp án A đúng.
+ \(\left\{ \begin{array}{l}CK \bot AB\\CK \bot SA\end{array} \right. \Rightarrow CK \bot \left( {SAB} \right)\) \( \Rightarrow CK \bot SB\).
+ \(\left\{ \begin{array}{l}SB \bot CK\\SB \bot CH\end{array} \right. \Rightarrow SB \bot \left( {CHK} \right) \Rightarrow SB \bot HK\).
CMTT: \(SC \bot HK \Rightarrow HK \bot \left( {SBC} \right)\), suy ra đáp án B đúng.
+ Gọi \(M = SH \cap BC\). Vì \(BC \bot \left( {SAH} \right)\,\,\left( {cmt} \right) \Rightarrow BC \bot AM\).
Mà K là trực tâm của tam giác ABC \( \Rightarrow K \in AM\), do đó SH, AK, BC đồng quy tại M, suy ra đáp án D đúng.
Chọn C.







