Phương pháp giải:

- Gọi H là trung điểm của AB, chứng minh \(SH \bot \left( {ABCD} \right)\).

- Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách từ đường thẳng này đến mặt phẳng chứa đường thẳng kia và song song với đường thẳng này. Từ đó chứng minh \(d\left( {BC;SD} \right) = d\left( {BC;\left( {SAD} \right)} \right) = d\left( {B;\left( {SAD} \right)} \right)\).

- Sử dụng phương pháp đổi điểm: \(AB \cap \left( P \right) = M \Rightarrow \dfrac{{d\left( {A;\left( P \right)} \right)}}{{d\left( {B;\left( P \right)} \right)}} = \dfrac{{AM}}{{BM}}\), đổi về tính khoảng cách từ chân đường vuông góc.

- Áp dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.

Lời giải chi tiết:

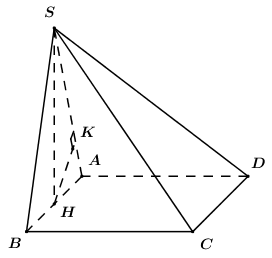
Gọi H là trung điểm của AB, do tam giác SAB đều nên \(SH \bot AB\).

Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\SH \subset \left( {SAB} \right),\,\,SH \bot AB\end{array} \right.\) \( \Rightarrow SH \bot \left( {ABCD} \right)\).

Vì ABCD là hình chữ nhật nên \(BC\parallel AD \Rightarrow BC\parallel \left( {SAD} \right) \supset SD\).

\( \Rightarrow d\left( {BC;SD} \right) = d\left( {BC;\left( {SAD} \right)} \right) = d\left( {B;\left( {SAD} \right)} \right)\).

Ta có: \(BH \cap \left( {SAD} \right) = A \Rightarrow \dfrac{{d\left( {B;\left( {SAD} \right)} \right)}}{{d\left( {H;\left( {SAD} \right)} \right)}} = \dfrac{{BA}}{{HA}} = 2\).

\( \Rightarrow d\left( {B;\left( {SAD} \right)} \right) = 2d\left( {H;\left( {SAD} \right)} \right)\).

Trong (SAB) kẻ \(HK \bot SA\,\,\left( {K \in SA} \right)\) ta có:

 \(\begin{array}{l}\left\{ \begin{array}{l}AD \bot SH\\AD \bot AB\end{array} \right. \Rightarrow AD \bot \left( {SAB} \right) \Rightarrow AD \bot HK\\\left\{ \begin{array}{l}HK \bot SA\\HK \bot AD\end{array} \right. \Rightarrow HK \bot \left( {SAD} \right)\\ \Rightarrow d\left( {H;\left( {SAD} \right)} \right) = HK\end{array}\)

Tam giác SAB đều cạnh 2a nên \(SH = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \).

Áp dụng hệ thức lượng trong tam giác vuông SAH có: \(HK = \dfrac{{SH.AH}}{{\sqrt {S{H^2} + A{H^2}} }} = \dfrac{{a\sqrt 3 .a}}{{\sqrt {3{a^2} + {a^2}} }} = \dfrac{{a\sqrt 3 }}{2}\).

Vậy \(d\left( {BC;SD} \right) = 2HK = a\sqrt 3 \).

Chọn A.