 Môn Toán - Lớp 12
Môn Toán - Lớp 12
 40 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ vận dụng, vận dụng cao
40 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ vận dụng, vận dụng cao
Câu hỏi
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;4} \right]\) và có đồ thị như hình vẽ
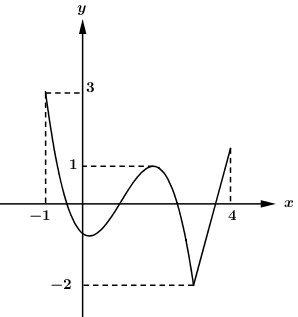
Có tất cả bao nhiêu giá trị nguyên của m thuộc đoạn \(\left[ { - 10;10} \right]\) để bất phương trình \(\left| {f\left( x \right) + m} \right| < 2m\) đúng với mọi x thuộc đoạn \(\left[ { - 1;4} \right]\)?
- A \(6\)
- B \(5\)
- C \(7\)
- D \(8\)
Phương pháp giải:
- Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.
Lời giải chi tiết:
Ta có: \(\left| {f\left( x \right) + m} \right| < 2m \Leftrightarrow - 2m < f\left( x \right) + m < 2m \Leftrightarrow - 3m < f\left( x \right) < m\).
\( \Leftrightarrow \left\{ \begin{array}{l} - 3m < \mathop {\min }\limits_{\left[ { - 1;4} \right]} f\left( x \right)\\\mathop {\max }\limits_{\left[ { - 1;4} \right]} f\left( x \right) < m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 3m < - 2\\3 < m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > \dfrac{2}{3}\\m > 3\end{array} \right. \Leftrightarrow m > 3\).
Kết hợp điều kiện đề bài \( \Rightarrow m \in \left( {3;10} \right],\,\,m \in \mathbb{Z} \Rightarrow m \in \left\{ {4;5;6;7;8;9;10} \right\}\).
Vậy có 7 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn C.






