Câu hỏi
Cho hình nón có bán kính đáy R, góc ở đỉnh là \(2\alpha \) với \({45^0} < \alpha < {90^0}\). Tính diện tích xung quanh của hình nón theo R và \(\alpha \).
- A \(\dfrac{{4\pi {a^2}}}{{\sin \alpha }}\)
- B \(\dfrac{{2\pi {a^2}}}{{\sin \alpha }}\)
- C \(\dfrac{{\pi {a^2}}}{{\sin \alpha }}\)
- D \(\dfrac{{\pi {a^2}}}{{3\sin \alpha }}\)
Phương pháp giải:
- Dựa vào thiết diện qua trục xác định đường sinh \(l\) và bán kính \(r\) của hình nón.
- Diện tích xung quanh của hình nón có đường sinh \(l\) và bán kính \(r\) là \({S_{xq}} = \pi rl\).
Lời giải chi tiết:
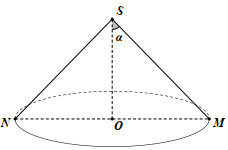
Theo bài ra ta có: \(\angle NSM = 2\alpha \Rightarrow \angle OSM = \alpha \).
Xét tam giác vuông SOM ta có: \(l = SM = \dfrac{{OM}}{{\sin \alpha }} = \dfrac{R}{{\sin \alpha }}\).
Vậy diện tích xung quanh của hình nón là \({S_{xq}} = \pi .R.\dfrac{R}{{\sin \alpha }} = \dfrac{{\pi {R^2}}}{{\sin \alpha }}\).
Chọn C.
Câu hỏi trước
