Phương pháp giải:

- Xác định khoảng cách từ tâm mặt đáy hình nón đến \(\left( \alpha  \right)\).

- Sử dụng định lí Pytago và hệ thức lượng trong tam giác vuông tính bán kính đáy \(r\) và đường sinh \(l\) của hình nón.

- Diện tích xung quanh của hình nón có kính đáy \(r\) và đường sinh \(l\) là: \({S_{xq}} = \pi rl\).

Lời giải chi tiết:

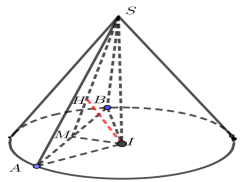
Gọi thiết diện của hình nón cắt bởi \(\left( \alpha  \right)\) là tam giác đều \(SAB\) và \(I\) là tâm đáy của hình nón.

Gọi \(M\) là trung điểm của \(AB\) ta có \(IM \bot AB\).

Ta có: \(\left\{ \begin{array}{l}AB \bot IM\\AB \bot SI\end{array} \right. \Rightarrow AB \bot \left( {SIM} \right)\).

Trong \(\left( {SIM} \right)\) kẻ \(IH \bot SM\,\,\left( {H \in SM} \right)\) ta có: \(\left\{ \begin{array}{l}HI \bot AB\,\,\left( {AB \bot \left( {SIM} \right)} \right)\\IH \bot SM\end{array} \right.\) \( \Rightarrow IH \bot \left( {SAB} \right)\).

\( \Rightarrow d\left( {I;\left( {SAB} \right)} \right) = IH = \dfrac{2}{{\sqrt 3 }}\).

Áp dụng hệ thức lượng trong tam giác vuông \(SIM\) ta có:

\(\dfrac{1}{{M{I^2}}} = \dfrac{1}{{I{H^2}}} - \dfrac{1}{{S{I^2}}} = \dfrac{3}{4} - \dfrac{1}{2} = \dfrac{1}{4} \Rightarrow MI = 2\).

Áp dụng định lí Pytago trong tam giác vuông \(SIM\) ta có: \(SM = \sqrt {S{I^2} + M{I^2}}  = \sqrt {2 + 4}  = \sqrt 6 \).

Vì \(SM\) là đường cao trong tam giác đều \(ABC\) nên \(SM = \dfrac{{AB\sqrt 3 }}{2} \Rightarrow AB = \dfrac{{2SM}}{{\sqrt 3 }} = 2\sqrt 2  = SA = l\).

\( \Rightarrow AM = \dfrac{1}{2}AB = \sqrt 2 \).

Áp dụng định lí Pytago trong tam giác vuông \(AIM\) ta có: \(r = IA = \sqrt {I{M^2} + A{M^2}}  = \sqrt {4 + 2}  = \sqrt 6 \).

Vậy diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl = \pi .\sqrt 6 .2\sqrt 2  = 4\pi \sqrt 3 \).

Chọn D.