Phương pháp giải:

- Gọi \(H,\,\,K\) lần lượt là hình chiếu của A, B lên (P).

- Sử dụng định lí Ta-lét chứng minh \(\dfrac{{AM}}{{BM}} = \dfrac{{AH}}{{BK}} = \dfrac{{d\left( {A;\left( P \right)} \right)}}{{d\left( {B;\left( P \right)} \right)}}\).

- Tính khoảng cách từ A đến (P): Khoảng cách từ \(A\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):\,\,Ax + By + Cz + D = 0\) là \({x^3} - x = x - {x^2} \Leftrightarrow {x^3} + {x^2} - 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x =  - 2\end{array} \right.\).

Lời giải chi tiết:

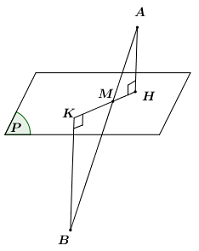
Vì \(\overrightarrow {AB}  = 3\overrightarrow {AM}  \Rightarrow A;\,\,B\) nằm hai phía của mặt phẳng \(\left( P \right)\) và \(\dfrac{{AM}}{{BM}} = \dfrac{1}{2}\).

Gọi H, K lần lượt là hình chiếu của A, B lên (P). Khi đó ta có AH // BK. Áp dụng định lí Ta-lét ta có: \(\dfrac{{AM}}{{BM}} = \dfrac{{AH}}{{BK}} = \dfrac{{d\left( {A;\left( P \right)} \right)}}{{d\left( {B;\left( P \right)} \right)}} = \dfrac{1}{2}\).

Mà \(d\left( {A;\left( P \right)} \right) = \dfrac{{\left| {3.2 + 4.4 - 12\left( { - 1} \right) + 5} \right|}}{{\sqrt {{3^2} + {4^2} + {{\left( { - 12} \right)}^2}} }} = 3\).

Vậy \(d\left( {B;\left( P \right)} \right) = 2d\left( {A;\left( P \right)} \right) = 6.\)

Chọn C.