Câu hỏi
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị hàm số như hình bên:
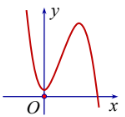
Khẳng định nào sau đây là đúng?
- A \(a < 0,\,\,b < 0,\,\,c = 0,\,\,d > 0\)
- B \(a < 0,\,\,c > 0,\,\,d > 0,\,\,b < 0\)
- C \(a < 0,\,\,b > 0,\,\,c > 0,\,\,d > 0\)
- D \(a < 0,\,\,b > 0,\,\,d > 0,\,\,c = 0\)
Phương pháp giải:
- Dựa vào \(\mathop {\lim }\limits_{x \to + \infty } y\) để xác định dấu của hệ số \(a\).
- Dựa vào giao điểm của đồ thị hàm số và trục tung để xác định dấu của hệ số \(d\).
- Dựa vào tổng và tích các cực trị để xác định dấu của hệ số \(b,\,\,c\).
- Sử dụng định nghĩa các đường tiệm cận của đồ thị hàm số \(y = f\left( x \right)\).
Lời giải chi tiết:
Vì nhánh cuối cùng của đồ thị hàm số đi xuống nên \(a < 0\), loại đáp án B.
Vì đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên \(d > 0\), loại đáp án B.
Dựa vào đồ thị hàm số ta thấy hàm số có 2 điểm cực trị \({x_1} = 0,\,\,{x_2} > 0\).
\( \Rightarrow \) Phương trình \(y' = 3a{x^2} + 2bx + c = 0\) có 2 nghiệm phân biệt thỏa mãn \({x_1} = 0,\,\,{x_2} > 0\).
\( \Leftrightarrow \left\{ \begin{array}{l}{b^2} - 3ac > 0\\{x_1} + {x_2} = \dfrac{{ - 2b}}{{3a}} > 0\\{x_1}{x_2} = \dfrac{c}{{3a}} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a < 0\\b > 0\\c = 0\end{array} \right.\).
Chọn D.







