Câu hỏi
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào?
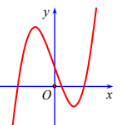
- A \(y = {x^3} + 3x + 1\)
- B \(y = - {x^3} + 3x - 1\)
- C \(y = {x^3} - 3x + 1\)
- D \(y = - {x^4} - 4{x^2} + 1\)
Phương pháp giải:
- Dựa vào hình dáng đồ thị, xác định đây là đồ thị hàm bậc ba hay bậc bốn để loại đáp án.
- Dựa vào hướng đi của nhánh cuối cùng, suy ra dấu của hệ số \(a\) để loại đáp án.
- Dựa vào số cực trị của hàm số để chọn đáp án đúng.
Lời giải chi tiết:
Đây là đồ thị hàm đa thức bậc ba nên loại đáp án D.
Vì nhánh cuối cùng của đồ thị hàm số đi lên nên hệ số \(a > 0\), do đó loại đáp án B.
Xét đáp án C có \(y' = 3{x^2} - 3 = 0 \Leftrightarrow x = \pm 1\), do đó hàm số có 2 cực trị thỏa mãn.
Chọn C.







