Phương pháp giải:

- Tìm ĐKXĐ.

- Cô lập \(m\), đưa phương trình về dạng \(f\left( x \right) = m\). Khi đó số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\) có tính chất song song với trục hoành.

- Khảo sát và lập BBT của hàm số \(y = f\left( x \right)\) và kết luận.

Lời giải chi tiết:

ĐKXĐ: \(9 - {x^2} \ge 0 \Leftrightarrow  - 3 \le x \le 3\).

Ta có: \(x - m - \sqrt {9 - {x^2}}  = 0 \Leftrightarrow x - \sqrt {9 - {x^2}}  = m\,\,\left( * \right)\). Khi đó số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = x - \sqrt {9 - {x^2}} \) và đường thẳng \(y = m\) có tính chất song song với trục hoành.

Xét hàm số \(y = x - \sqrt {9 - {x^2}} \) với \( - 3 \le x \le 3\) ta có \(y' = 1 + \dfrac{x}{{\sqrt {9 - {x^2}} }} = \dfrac{{\sqrt {9 - {x^2}}  + x}}{{\sqrt {9 - {x^2}} }}\).

Cho \(y' = 0 \Leftrightarrow \sqrt {9 - {x^2}}  + x = 0\) \( \Leftrightarrow \sqrt {9 - {x^2}}  =  - x\) \( \Leftrightarrow \left\{ \begin{array}{l} - x \ge 0\\9 - {x^2} = {x^2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \le 0\\x =  \pm \dfrac{{3\sqrt 2 }}{2}\end{array} \right.\) \( \Leftrightarrow x =  - \dfrac{{3\sqrt 2 }}{2}\).

Ta có BBT:

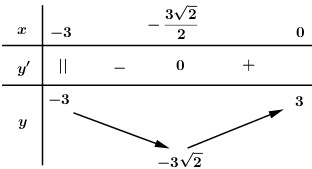
Dựa vào BBT ta thấy phương trình (*) có đúng 1 nghiệm khi và chỉ khi \(m =  - 3\sqrt 2 \).

Vậy \(m =  - 3\sqrt 2 \).

Chọn D.