Phương pháp giải:

Công thức tính thể tích khối nón có bán kính đáy \(r\) và chiều cao \(h\) là \(V = \dfrac{1}{3}\pi {r^2}h.\)

Lời giải chi tiết:

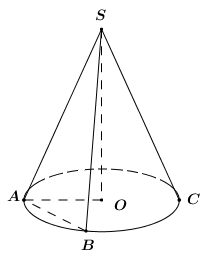
Gọi hình nón có đỉnh \(S\) như hình vẽ.

Khi đó ta có thiết diện là \(\Delta SAB\) đều.

\(\begin{array}{l} \Rightarrow {S_{SAB}} = 9\sqrt 3  \Leftrightarrow \dfrac{{S{A^2}.\sqrt 3 }}{4} = 9\sqrt 3  \Leftrightarrow SA = 6.\\ \Rightarrow SA = SB = AB = 6\end{array}\)

Gọi \(H\) là trung điểm của \(AB \Rightarrow OH \bot AB\) và \(AH = \dfrac{1}{2}AB = 3\).

Áp dụng định lí Pytago trong tam giác vuông \(SOA\) ta có:

\(OA = \sqrt {S{A^2} - S{O^2}}  = \sqrt {{6^2} - {{\left( {2\sqrt 5 } \right)}^2}}  = 4 = r\).

Vậy thể tích khối nón là \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {4^2}.2\sqrt 5  = \dfrac{{32\sqrt 5 \pi }}{3}\).

Chọn A.