Câu hỏi
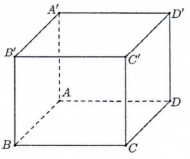
Cho khối lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy là hình thoi cạnh \(a\), \(BD = \sqrt 3 a\) và \(AA' = 4a\) (minh họa như hình bên). Thể tích của khối lăng trụ đã cho bằng
- A \(2\sqrt 3 \,{a^3}.\)
- B \(4\sqrt 3 {a^3}.\)
- C \(\dfrac{{a\sqrt 3 {a^3}}}{3}.\)
- D \(\dfrac{{4\sqrt 3 {a^3}}}{3}.\)
Phương pháp giải:
- Tính diện tích tam giác \(ABD\), sử dụng công thức He-rong \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \) với \(p\) là nửa chu vi tam giác, \(a,\,\,b,\,\,c\) là độ dài 3 cạnh của tam giác.
- Suy ra \({S_{ABCD}} = 2{S_{ABD}}\).
- Tính thể tích khối lăng trụ \(V = AA'.{S_{ABCD}}\).
Lời giải chi tiết:
Gọi \(p\) là nửa chu vi tam giác \(ABD\), ta có \(p = \dfrac{{AB + AD + BD}}{2} = \dfrac{{a + a + a\sqrt 3 }}{2} = \dfrac{{2 + \sqrt 3 }}{2}a\).
Diện tích tam giác \(ABD\) là: \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \dfrac{{{a^2}\sqrt 3 }}{4}\).
\( \Rightarrow {S_{ABCD}} = 2{S_{ABD}} = \dfrac{{{a^2}\sqrt 3 }}{2}\).
Vậy \({V_{ABCD}} = AA'.{S_{ABCD}} = 4a.\dfrac{{{a^2}\sqrt 3 }}{2} = 2{a^3}\sqrt 3 \).
Chọn A.