Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông có cạnh bằng \(a\), cạnh bên \(SA\) vuông góc với mặt phẳng đáy và \(SA = a\sqrt 2 \) (hình bên). Gọi \(H,\,\,K\) lần lượt là hình chiếu vuông góc của \(A\) trên \(SB,\,\,SD\). Số đo của góc tạo bởi mặt phẳng \(\left( {AHK} \right)\) và \(\left( {ABCD} \right)\) bằng:
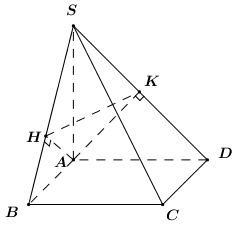
- A \({90^0}\)
- B \({60^0}\)
- C \({30^0}\)
- D \({45^0}\)
Phương pháp giải:
- Sử dụng kết quả sau: \(\left\{ \begin{array}{l}d \bot \left( P \right)\\d' \bot \left( Q \right)\end{array} \right. \Rightarrow \angle \left( {\left( P \right);\left( Q \right)} \right) = \angle \left( {d;d'} \right)\).
- Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.
Lời giải chi tiết:
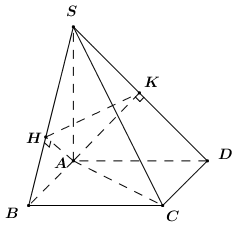
Ta có: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH\)
\(\left\{ \begin{array}{l}AH \bot SB\\AH \bot BC\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC\).
Chứng minh tương tự ta có: \(AK \bot \left( {SCD} \right) \Rightarrow AK \bot SC\).
\( \Rightarrow SC \bot \left( {AHK} \right)\).
Ta có: \(SA \bot \left( {ABCD} \right),\,\,SC \bot \left( {AHK} \right)\) \( \Rightarrow \angle \left( {\left( {AHK} \right);\left( {ABCD} \right)} \right) = \angle \left( {SC;AC} \right)\).
Vì \(ABCD\) là hình vuông cạnh \(a\) nên \(AC = a\sqrt 2 \). Lại có \(SA = a\sqrt 2 \) nên \(\Delta SAC\) vuông cân tại \(A\).
\( \Rightarrow \angle \left( {SC;AC} \right) = \angle SCA = {45^0}\) hay \(\angle \left( {\left( {AHK} \right);\left( {ABCD} \right)} \right) = {45^0}\).
Chọn D.







