Câu hỏi
Cho tứ diện \(OABC\) có \(OA,\,\,OB,\,\,OC\) đôi một vuông góc với nhau (hình bên). Gọi \(H\) là hình chiếu vuông góc của \(O\) trên mặt phẳng \(\left( {ABC} \right)\). Khẳng định nào sau đây là khẳng định sai?
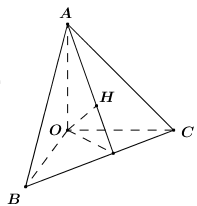
- A \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}\)
- B \(H\) là trực tâm tam giác \(ABC\)
- C \(OA \bot BC\)
- D \(AH \bot \left( {OBC} \right)\)
Phương pháp giải:
- Sử dụng các định lí: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right),\,\,\forall \Delta \subset \left( P \right) \Rightarrow d \bot \Delta \).
- Sử dụng hệ thức lượng trong tam giác vuông.
Lời giải chi tiết:
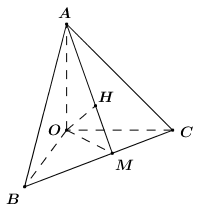
Gọi \(M = AH \cap BC\) ta có: \(\left\{ \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right. \Rightarrow OA \bot \left( {OBC} \right) \Rightarrow OA \bot BC\), suy ra đáp án C đúng.
\(\left\{ \begin{array}{l}BC \bot OA\\BC \bot OH\,\,\left( {OH \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow BC \bot \left( {OAM} \right)\).
\( \Rightarrow BC \bot AM\) hay \(AH \bot BC\) tại \(M\).
Chứng minh tương tự ta có: \(BH \bot AC,\,\,CH \bot AB\).
Do đó \(H\) là trực tâm của \(\Delta ABC\) nên đáp án B đúng.
Ta có: \(BC \bot \left( {OAM} \right)\,\,\left( {cmt} \right) \Rightarrow BC \bot OM\).
\(OH \bot \left( {ABC} \right)\,\,\left( {gt} \right) \Rightarrow OH \bot AM\).
Áp dụng hệ thức lượng trong các tam giác vuông ta có:
\(\begin{array}{l}\dfrac{1}{{O{M^2}}} = \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}\\\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{M^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}\end{array}\)
Do đó đáp án A đúng.
Vậy đáp án D sai.
Chọn D.







