Câu hỏi
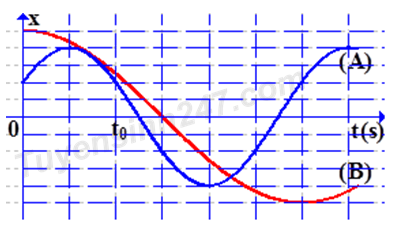
Hai vật nhỏ A và B dao động điều hòa có đồ thị mô tả li độ theo thời gian như hình vẽ. tại thời điểm t0, tỉ số tốc độ của A đối với tốc độ của B là
- A 8/5.
- B 2.
- C 1/2.
- D 5/8.
Phương pháp giải:
+ Đọc đồ thị x – t
+ Viết phương trình dao động từ đồ thị
+ Xác định thời điểm trên đồ thị
Lời giải chi tiết:
Gọi 1 ô theo trục Ox là A, 1 ô theo trục Ot là a
Ta có:
+ Biên độ của A là \(2A\) , biên độ của B là \(5A\)
+ Chu kì, dao động của A là \(6a\), chu kì dao động của B là \(T = 12a\)
\( \Rightarrow {\omega _A} = 2{\omega _B}\)
Phương trình dao động của A: \({x_A} = 4Acos\left( {{\omega _A}t - \dfrac{\pi }{3}} \right)\)
Phương trình dao động của vật B: \({x_B} = 5Acos\left( {\dfrac{{{\omega _A}}}{2}t} \right)\)
Tốc độ của A và B tại thời điểm \({t_0} = \dfrac{{2{T_A}}}{6} = \dfrac{{{T_A}}}{3}\) là:
\(\left\{ \begin{array}{l}{v_A} = - 4A{\omega _A}\sin \left( {{\omega _A}\dfrac{{{T_A}}}{3} - \dfrac{\pi }{3}} \right) = - 4A{\omega _A}\sin \left( {\dfrac{\pi }{3}} \right)\\{v_B} = - 5A\dfrac{{{\omega _A}}}{2}\sin \left( {\dfrac{{{\omega _A}}}{2}\dfrac{{{T_A}}}{3}} \right) = - 5A\dfrac{{{\omega _A}}}{2}\sin \left( {\dfrac{\pi }{3}} \right)\end{array} \right.\)
\( \Rightarrow \dfrac{{{v_A}}}{{{v_B}}} = \dfrac{{ - 4A{\omega _A}\sin \left( {\dfrac{\pi }{3}} \right)}}{{ - 5A\dfrac{{{\omega _A}}}{2}\sin \left( {\dfrac{\pi }{3}} \right)}} = \dfrac{8}{5}\)
Chọn A