Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(2a\) và \(SA\) vuông góc với đáy. Biết khoảng cách giữa \(AC\) và \(SB\) bằng \(a\). Tính thể tích khối chóp \(S.ABCD\).
- A \(\dfrac{{2\sqrt 2 {a^3}}}{3}\)
- B \(\dfrac{{4\sqrt 2 {a^3}}}{3}\)
- C \(\sqrt 2 {a^3}\)
- D \(\dfrac{{3{a^3}}}{{\sqrt 2 }}\)
Phương pháp giải:
- Khoảng cách giữa hai đường thẳng chéo nhau \(d\) và \(d'\) là khoảng cách từ 1 điểm trên \(d\) tới mặt phẳng \(\left( \alpha \right)\) đi qua \(d'\) và song song với \(d\).
- Dựa vào khoảng cách giữa \(AC\) và \(SB\) để tính độ dài \(SA\) và thể tích khối chóp.
Lời giải chi tiết:
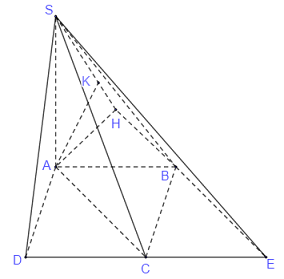
Qua \(B\), kẻ \(BE\parallel AC\,\,\left( {E \in DC} \right)\). Ta có: \(AC\parallel \left( {SBE} \right) \supset SB\).
Suy ra \(d\left( {AC;SB} \right) = d\left( {AB;\left( {SBE} \right)} \right) = d\left( {A;\left( {SBE} \right)} \right).\)
Qua \(A,\) kẻ \(AH \bot BE\,\,\,\,\left( {H \in BE} \right);\)\(AK \bot SH\left( {K \in SH} \right)\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BE\\AH \bot BE\end{array} \right\} \Rightarrow BE \bot \left( {SAH} \right) \Rightarrow BE \bot AK\\AK \bot AH \Rightarrow AK \bot \left( {SBE} \right)\\ \Rightarrow d\left( {AC;SB} \right) = d\left( {A;\left( {SBE} \right)} \right) = AK\\ \Rightarrow AK = a.\end{array}\)
Vì \(BE\parallel AC \Rightarrow \angle CBE = \angle ACB = {45^0}\) (so le trong).
\(\begin{array}{l} \Rightarrow \angle ABH = {180^0} - \angle ABC - \angle CBE\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {180^0} - {90^0} - {45^0} = {45^0}.\end{array}\)
Do đó, tam giác \(AHB\) vuông cân tại \(H\). Suy ra \(AH = HB = \dfrac{{AB}}{{\sqrt 2 }} = \sqrt 2 a.\)
Tam giác \(SAH\) vuông tại \(A\) có đường cao \(AK\) nên:
\(\dfrac{1}{{A{K^2}}} = \dfrac{1}{{A{S^2}}} + \dfrac{1}{{A{H^2}}}\) (Hệ thức lượng)
\( \Leftrightarrow \dfrac{1}{{{a^2}}} = \dfrac{1}{{A{S^2}}} + \dfrac{1}{{{{\left( {\sqrt 2 a} \right)}^2}}} \Rightarrow SA = a\sqrt 2 .\)
Vậy thể tích của khối chóp đã cho là: \({V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}.\sqrt 2 a.{\left( {2a} \right)^2} = \dfrac{{4\sqrt 2 {a^3}}}{3}.\)
Chọn B.







