Câu hỏi
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;3} \right]\) có đồ thị như hình vẽ bên. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 1;3} \right]\). Giá trị của \(M - m\) bằng:
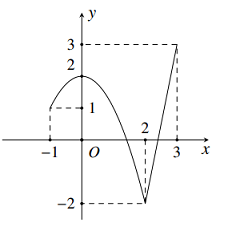
- A \(0\)
- B \(1\)
- C \(4\)
- D \(5\)
Phương pháp giải:
Hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) có :
+) \(f\left( x \right) \ge m,\,\forall x \in \left[ {a;b} \right];\,\,\,f\left( {{x_0}} \right) = m,\,\,{x_0} \in \left[ {a;b} \right]\) thì \(\mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right) = m\)
+) \(f\left( x \right) \le M,\,\forall x \in \left[ {a;b} \right];\,\,\,f\left( {{x_1}} \right) = M,\,\,{x_1} \in \left[ {a;b} \right]\) thì \(\mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right) = M\)
Lời giải chi tiết:
Từ đồ thị hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 1;3} \right]\) ta thấy :
+) \(f\left( x \right) \ge - 2,\,\forall x \in \left[ { - 1;3} \right];\,\,\,f\left( 2 \right) = - 2\) nên \(m = \mathop {\min }\limits_{\left[ { - 1;3} \right]} f\left( x \right) = - 2.\)
+) \(f\left( x \right) \le 3,\,\forall x \in \left[ { - 1;3} \right];\,\,\,f\left( 3 \right) = 3\) nên \(M = \mathop {\max }\limits_{\left[ { - 1;3} \right]} f\left( x \right) = 3.\)
Vậy \(M - m = 3 - \left( { - 2} \right) = 5.\)
Chọn D.







