Câu hỏi
Cho lăng trụ đứng \(ABC.A'B'C'\) với \(ABC\) là tam giác vuông cân tại \(C\) có \(AB = a\) , mặt bên \(ABB'A'\) là hình vuông. Mặt phẳng qua trung điểm \(I\) của \(AB\) và vuông góc với \(AB'\) chi khối lăng trụ thành 2 phần. Tính thể tích mỗi phần?
- A \({V_1} = \dfrac{{{a^3}}}{{48}},\,\,\,{V_2} = \dfrac{{11{a^3}}}{{24}}\)
- B \({V_1} = \dfrac{{{a^3}}}{{24}},\,\,\,{V_2} = \dfrac{{11{a^3}}}{{48}}\)
- C \({V_1} = \dfrac{{{a^3}}}{{48}},\,\,\,{V_2} = \dfrac{{11{a^3}}}{{48}}\)
- D \({V_1} = \dfrac{{{a^3}}}{{24}},\,\,\,{V_2} = \dfrac{{5{a^3}}}{{24}}\)
Phương pháp giải:
- Dựng mặt phẳng đi qua \(I\) và vuông góc với \(AB'\) (là mặt phẳng \(\left( {DIC} \right)\) với \(D\) là trung điểm của \(AA'\).
- Tính diện tích tam giác \(ABC\), từ đó suy ra diện tích tam giác \(AIC\).
- Tính độ dài đường cao \(A'A\) của lăng trụ và độ dài đường cao \(DA\) của hình chóp \(D.AIC\).
- Tính thể tích khối lăng trụ \(ABC.A'B'C'\) và khối chóp \(D.AIC\), từ đó tính được thể tích phần còn lại của khối lăng trụ được chia bởi mặt phẳng \(\left( {DIC} \right)\)
Lời giải chi tiết:
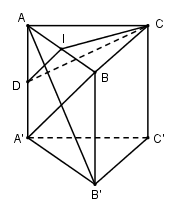
Gọi \(D\) là trung điểm của \(AA'\) ta có \(ID\) là đường trung bình của tam giác \(AA'B\)\( \Rightarrow ID\parallel A'B\).
Mà \(A'B \bot AB'\) (do \(ABB'A'\) là hình vuông) \( \Rightarrow ID \bot AB'\)
Tam giác \(ABC\) vuông cân tại \(C\) nên \(IC \bot AB\). Mà \(AA' \bot \left( {ABC} \right) \Rightarrow AA' \bot IC\)
\( \Rightarrow IC \bot \left( {ABB'A'} \right) \Rightarrow IC \bot AB'\)
\( \Rightarrow AB' \bot \left( {ICD} \right)\)
\( \Rightarrow \) Mặt phẳng qua \(I\) và vuông góc với \(AB'\) là \(\left( {ICD} \right).\)
Tam giác \(ABC\) vuông cân tại \(C\) nên \(AC = BC = \dfrac{{AB}}{{\sqrt 2 }} = \dfrac{a}{{\sqrt 2 }}\).
\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}AC.BC = \dfrac{1}{2}\dfrac{a}{{\sqrt 2 }}\dfrac{a}{{\sqrt 2 }} = \dfrac{{{a^2}}}{4}\).
Vì \(ABB'A'\) là hình vuông \( \Rightarrow AA' = AB = a.\)
\( \Rightarrow {V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = a.\dfrac{{{a^2}}}{4} = \dfrac{{{a^3}}}{4} = V\)
Ta có:
\(\begin{array}{l}{V_{D.ACI}} = \dfrac{1}{3}AD.{S_{ACI}} = \dfrac{1}{3}.\dfrac{1}{2}AA'.\dfrac{1}{2}{S_{ABC}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{{12}}{V_{ABC.A'B'C'}} = \dfrac{1}{{12}}.\dfrac{{{a^3}}}{4} = \dfrac{{{a^3}}}{{48}} = {V_1}\end{array}\)
\( \Rightarrow {V_2} = V - {V_1} = \dfrac{{{a^3}}}{4} - \dfrac{{{a^3}}}{{48}} = \dfrac{{11{a^3}}}{{48}}.\)
Chọn C.







