Câu hỏi
Một lò xo nhẹ có độ cứng 100N/m, đầu trên gắn cố định, đầu dưới treo quả cầu nhỏ có khối lượng m = 1kg sao cho vật có thể dao động không ma sát theo phương thẳng đứng trùng với trục của lò xo. Lúc đầu dùng giá nằm ngang đỡ m để lò xo không biến dạng. Sau đó cho giá đỡ chuyển động thẳng đứng xuống dưới nhanh dần đều với gia tốc 2m/s2. Bỏ qua mọi ma sát. Lấy gia tốc trọng trường g = 10m/s2. Khi m rời khỏi giá đỡ nó dao động điều hòa. Biên độ dao động điều hòa là
- A 1,5cm
- B 2cm
- C 6cm
- D 1,2cm
Phương pháp giải:
Vẽ hình biểu diễn các lực tác dụng vào vật nặng khi vật năng di chuyển.
Áp dụng định luật II Niu- tơn:
\(\overrightarrow P + \overrightarrow N + \overrightarrow F = m.\overrightarrow a \)
Khi vật rời khỏi tấm ván đỡ thì phản lực \(\overrightarrow N \) = 0.
Ta tìm được vị trí vật rời khỏi giá đỡ thì lò xo giãn ∆l, khi đó
Vị trí cân bằng là vị trí lò xo giãn ∆l0thỏa mãn: \(\Delta {l_0} = \frac{{mg}}{k}\)
Lời giải chi tiết:
Ta có hình vẽ:
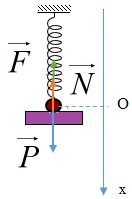
Áp dụng định luật II Niu- tơn: \(\overrightarrow P + \overrightarrow N + \overrightarrow F = m.\overrightarrow a \)
Khi vật rời khỏi tấm ván đỡ thì phản lực \(\overrightarrow N \) = 0.
Ta có : \(\overrightarrow F + \overrightarrow P = m\overrightarrow a \)
Chiếu lên Ox ta được:
\(\begin{array}{l}
- F + P = ma \Rightarrow F = P - ma = mg - ma\\
\Rightarrow k.\Delta l = F \Rightarrow \Delta l = \frac{F}{k} = \frac{{mg - ma}}{k} = 0,08m = 8cm
\end{array}\)
Vị trí cân bằng là vị trí lò xo giãn ∆l0 thỏa mãn:
\(\Delta {l_0} = \frac{{mg}}{k} = \frac{{1.10}}{{100}} = 0,1m = 10cm\)
Vậy li độ của dao động là:
\(x = 8-10 = - 2cm\)
Vận tốc của vật khi đó là
\(v = \sqrt {2as} = \sqrt {2.2.8} = \sqrt {32} cm/s\)
Vậy biên độ dao động của vật là
\(A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} = 6cm\)
Chọn C.







