Phương pháp giải:

Điều kiện có cực đại giao thoa trong giao thoa sóng hai nguồn cùng pha:

\({d_2} - {d_1} = k\lambda ;k \in Z\)

Trên Ax có M là điểm cực đại xa nhất, nên nó là cực đại thuộc vân cực đại bậc 1 với k = 1; do đó N là vân cực đại bậc 2, với k = 2; P là vân cực đại bậc 3 với k = 3; Q là vân cực đại ứng với k_max.

Vẽ hình. Sử dụng các kiến thức toán học để biến đổi tìm bước sóng λ và AB;

Số điểm cực đại trên AB là số giá trị k thỏa mãn: 

\( - \frac{{AB}}{\lambda } \le k \le \frac{{AB}}{\lambda }\)

Lời giải chi tiết:

Trên Ax có M là điểm cực đại xa nhất, nên nó là cực đại thuộc vân cực đại bậc 1 với k = 1; do đó N là vân cực đại bậc 2, với k = 2; P là vân cực đại bậc 3 với k = 3; Q là vân cực đại ứng với k_max.

Ta có hình vẽ:

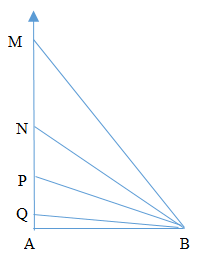
Ta xét các vị trí cực đại M, N, P:

\(\begin{array}{l}
MB - MA = \lambda \Rightarrow \sqrt {A{B^2} + M{A^2}} - MA = \lambda \\
\Rightarrow \sqrt {A{B^2} + M{A^2}} = \lambda + MA\\
\Rightarrow A{B^2} + M{A^2} = {\lambda ^2} + 2\lambda MA + M{A^2}\\
\Leftrightarrow A{B^2} = {\lambda ^2} + 2\lambda MA\,\,\,\,\,\,(1)\\
NB - NA = 2\lambda \Rightarrow \sqrt {A{B^2} + N{A^2}} - NA = 2\lambda \\
\Rightarrow \sqrt {A{B^2} + N{A^2}} = 2\lambda + NA\\
\Rightarrow A{B^2} + N{A^2} = 4{\lambda ^2} + 4\lambda NA + N{A^2}\\
\Leftrightarrow A{B^2} = 4{\lambda ^2} + 4\lambda NA\,\,\,\,\,\,(2)\\
PB - PA = 3\lambda \Rightarrow \sqrt {A{B^2} + P{A^2}} - PA = 3\lambda \\
\Rightarrow \sqrt {A{B^2} + P{A^2}} = 3\lambda + PA\\
\Rightarrow A{B^2} + P{A^2} = 9{\lambda ^2} + 6\lambda PA + P{A^2}\\
\Leftrightarrow A{B^2} = 4{\lambda ^2} + 6\lambda PA\,\,\,\,\,\,(3)
\end{array}\)

Từ (1) và (2) ta có:

\(\begin{array}{l}
{\lambda ^2} + 2\lambda MA = 4{\lambda ^2} + 4\lambda NA \Leftrightarrow \lambda + 2MA = 4\lambda + 4NA\\
\Rightarrow 2MN + 2NA = 3\lambda \,\,\,\left( 4 \right)
\end{array}\)

Từ (2) và (3) ta có:

\(\begin{array}{l}
4{\lambda ^2} + 4\lambda NA = 9{\lambda ^2} + 6\lambda PA \Rightarrow 4\lambda + 4NA = 9\lambda + 6PA\\
\Rightarrow 4NP - 2AP = 5\lambda \,\,\,\left( 5 \right)
\end{array}\)

Từ (4) và (5) ta có:

\(\begin{array}{l}
2\lambda = 4NP - 2MN + 2NP = 6NP - 2MN\\
\Rightarrow \lambda = 3NP - MN = 3.8,75 - 22,25 = {4_{}}cm
\end{array}\)

Thay vào (5) ta được:

\(4.8,75 - 2AP = 5.4 \Rightarrow AP = 7,{5_{}}cm\)

Thay vào (3) ta được:

\(AB = \sqrt {9.{\lambda ^2} + 6\lambda .AP} = \sqrt {{{9.4}^2} + 6.4.7,5} = {18_{}}cm\)

Số điểm cực đại trên AB là số giá trị k thỏa mãn:

\(\begin{array}{l}
- \frac{{AB}}{\lambda } \le k \le \frac{{AB}}{\lambda } \Rightarrow - \frac{{18}}{4} \le k \le \frac{{18}}{4} \Rightarrow - 4,5 \le k \le 4,5\\
\Rightarrow k = \pm 4; \pm 3; \pm 2; \pm 1;0
\end{array}\)

Vậy Q là điểm cực đại gần A nhất sẽ thuộc cực đại bậc 4, k = 4.

Ta có:

\(\begin{array}{l}
QB - QA = 4\lambda \Rightarrow \sqrt {A{B^2} + A{Q^2}} - AQ = 4\lambda \\
\Rightarrow A{B^2} + A{Q^2} = 16.{\lambda ^2} + 8\lambda AQ + A{Q^2}\\
\Rightarrow AQ = \frac{{A{B^2} - 16{\lambda ^2}}}{{8\lambda }} = 2,{1_{}}cm
\end{array}\)

Chọn C.