Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có bản biến thiên như sau :
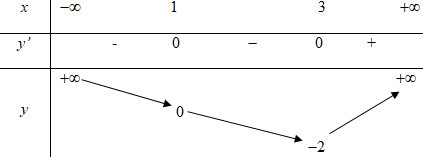
Hàm số \(g\left( x \right) = f\left( {{x^2} - 2x} \right)\) có bao nhiêu điểm cực trị?
- A \(5\)
- B \(3\)
- C \(2\)
- D \(4\)
Phương pháp giải:
- Tính \(g'\left( x \right)\), giải phương trình \(g'\left( x \right) = 0\).
- Xác định các nghiệm của phương trình \(g'\left( x \right) = 0\) mà qua đó \(g'\left( x \right)\) đổi dấu.
Lời giải chi tiết:
Ta có: \(g'\left( x \right) = \left( {2x - 2} \right)f'\left( {{x^2} - 2x} \right)\)
\(\begin{array}{l}g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\f'\left( {{x^2} - 2x} \right) = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} - 2x = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\\x = 3\end{array} \right.\end{array}\)
Ta không xét \({x^2} - 2x = 1\) do qua đó \(f'\left( x \right)\).
Vậy hàm số đã cho có 3 điểm cực trị.
Chọn B.







