Phương pháp giải:

- Đặt \(h\left( x \right) = 3{x^4} - 4{x^3} - 12{x^2} + m\), khảo sát và lập BBT của hàm số \(h\left( x \right)\) trên \(\left[ { - 1;3} \right]\).

- Chia các trường hợp, từ đó suy ra đồ thị hàm số \(y = \left| {h\left( x \right)} \right|\) và tìm GTLN của hàm số trên \(\left[ { - 1;3} \right]\).

- Tìm các giá trị của \(m\) thỏa mãn từng trường hợp.

Lời giải chi tiết:

Đặt \(h\left( x \right) = 3{x^4} - 4{x^3} - 12{x^2} + m\) ta có:

\(h'\left( x \right) = 12{x^3} - 12{x^2} - 24x = 0 \Rightarrow \left[ \begin{array}{l}x = 0\\x =  - 1\\x = 2\end{array} \right.\)

Bảng biến thiên:

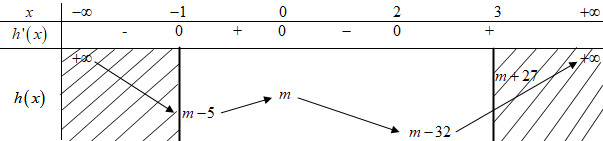
Ta thấy \(m - 32 < m - 5 < m < m + 27\).

TH1: \(m - 32 \ge 0 \Leftrightarrow m \ge 32\).

\( \Rightarrow M = m + 27 = \dfrac{{71}}{2} \Leftrightarrow m = \dfrac{{17}}{2}\,\,\left( {ktm} \right)\).

TH2: \(m - 32 < 0 \le m - 5 \Leftrightarrow 5 \le m < 32\).

\( \Rightarrow M \in \left\{ {32 - m;m + 27} \right\}\).

Nếu \(m + 27 \ge 32 - m \Leftrightarrow 2m \ge 5 \Leftrightarrow m \ge \dfrac{5}{2}\), kết hợp điều kiện \( \Rightarrow 5 \le m < 32\), khi đó \(M = m + 27 = \dfrac{{71}}{2} \Leftrightarrow m = \dfrac{{17}}{2}\,\,\,\left( {tm} \right)\).

Nếu \(m + 27 < 32 - m \Leftrightarrow m < \dfrac{5}{2}\), kết hợp điều kiện \( \Rightarrow m \in \emptyset \).

TH3: \(m - 5 < 0 \le m \Leftrightarrow 0 \le m < 5\).

 \( \Rightarrow M \in \left\{ {32 - m;m + 27} \right\}\).

Nếu \(m + 27 \ge 32 - m \Leftrightarrow 2m \ge 5 \Leftrightarrow m \ge \dfrac{5}{2}\), kết hợp điều kiện \( \Rightarrow \dfrac{5}{2} \le m < 5\), khi đó \(M = m + 27 = \dfrac{{71}}{2} \Leftrightarrow m = \dfrac{{17}}{2}\,\,\,\left( {ktm} \right)\).

Nếu \(m + 27 < 32 - m \Leftrightarrow m < \dfrac{5}{2}\), kết hợp điều kiện \( \Rightarrow 0 \le m < \dfrac{5}{2}\), khi đó \(M = 32 - m = \dfrac{{71}}{2} \Leftrightarrow m =  - \dfrac{7}{2}\,\,\left( {ktm} \right)\).

TH4: \(m + 27 \le 0 \Leftrightarrow m \le  - 27\), khi đó \(M = 32 - m = \dfrac{{71}}{2} \Leftrightarrow m =  - \dfrac{7}{2}\,\,\,\left( {tm} \right)\).

Vậy có hai giá trị của \(m\) thỏa mãn yêu cầu bài toán là \(m \in \left\{ {\dfrac{{17}}{2}; - \dfrac{7}{2}} \right\}\), tổng các giá trị của \(m\) là \(\dfrac{{17}}{2} + \left( { - \dfrac{7}{2}} \right) = \dfrac{{10}}{2} = 5\).

Chọn D.