Câu hỏi
Hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.
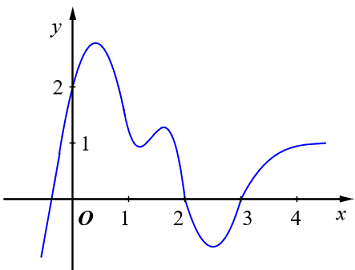
Số nghiệm của phương trình \(f\left( {{x^3} - 3x} \right) + 3{x^3} - 3x - 13 = {\left( {{x^2} - 2} \right)^3} - 3{\left( {x - 1} \right)^2}\) là:
- A \(3\).
- B \(4\).
- C \(5\)
- D \(6\)
Phương pháp giải:
Biến đổi, đưa phương trình về phương trình ẩn \(t = {x^3} - 3x\).
Lời giải chi tiết:
Ta có: \(f\left( {{x^3} - 3x} \right) + 3{x^3} - 3x - 13 = {\left( {{x^2} - 2} \right)^3} - 3{\left( {x - 1} \right)^2}\)\(\begin{array}{l} \Leftrightarrow f\left( {{x^3} - 3x} \right) + 3{x^3} - 3x - 13 = {x^6} - 6{x^4} + 12{x^2} - 8 - 3{x^2} + 6x - 3\\ \Leftrightarrow f\left( {{x^3} - 3x} \right) + 3{x^3} - 9x = {x^6} - 6{x^4} + 9{x^2} + 2 \Leftrightarrow f\left( {{x^3} - 3x} \right) = {\left( {{x^3} - 3x} \right)^2} - 3\left( {{x^3} - 3x} \right) + 2\,\,(*)\end{array}\)
Đặt \(t = {x^3} - 3x,\,\,t \in \mathbb{R}\). Phương trình trở thành: \(g\left( t \right) = {t^2} - 3t + 2\). Biểu diễn đồ thị của hàm số \(y = g\left( x \right)\) :
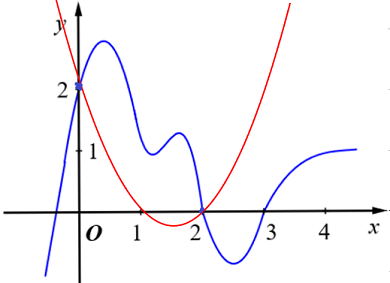
Từ đồ thị hàm số, ta có: \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}{x^3} - 3x = 0\\{x^3} - 3x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^3} - 3x = 0\\{x^3} - 3x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 3 \\x = - 1\\x = 2\end{array} \right.\)
Số nghiệm của phương trình đã cho là: 5.
Chọn C.







