Phương pháp giải:

- Tìm TXĐ của hàm số.

- Cô lập \(m\), lập BBT của hàm số và kết luận.

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\).

Ta có: \({2^x} + 3 = m\sqrt {{4^x} + 1} \) \( \Leftrightarrow m = \dfrac{{{2^x} + 3}}{{\sqrt {{4^x} + 1} }}\) (*)

Xét hàm số \(f\left( t \right) = \dfrac{{t + 3}}{{\sqrt {{t^2} + 1} }}\,\,\left( {t > 0} \right)\) ta có:

\(f'\left( t \right) = \dfrac{{1.\sqrt {{t^2} + 1}  - \dfrac{{t\left( {t + 3} \right)}}{{\sqrt {{t^2} + 1} }}}}{{{t^2} + 1}} = \dfrac{{1 - 3t}}{{\left( {{t^2} + 1} \right)\sqrt {{t^2} + 1} }}\),  \(f'\left( t \right) = 0 \Leftrightarrow t = \dfrac{1}{3}\)

BBT:

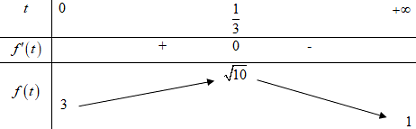
Tập giá trị của hàm số \(f\left( t \right)\) trên khoảng \(\left( {0; + \infty } \right)\) là \(\left( {1;\sqrt {10} } \right]\).

Để phương trình (*) có nghiệm thì \(m \in \)\(\left( {1;\sqrt {10} } \right] \Rightarrow a = 1,\,b = \sqrt {10}  \Rightarrow \)\({a^2} + 2{b^2} = 21\).

Chọn C.