Phương pháp giải:

Xác định số lượng tâm, bán kính của mặt cầu.

Lời giải chi tiết:

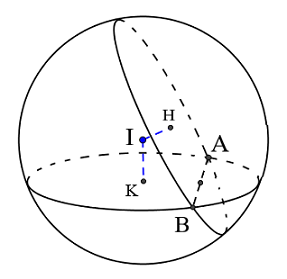
Gọi tâm của 2 đường tròn là \(H,\,\,K\) và \(I\) là tâm của mặt cầu chứa cả 2 đường tròn đó.

Nhận xét: \(I\) chính là giao điểm của hai đường vuông góc kẻ từ tâm các đường tròn, vuông góc với mặt phẳng chứa đường tròn đó.

Do đó, tâm \(I\)được xác định là duy nhất.

Vì 2 đường tròn nằm trên có chung dây cung AB nên AB cũng là 1 dây cung của mặt cầu.

\( \Rightarrow \) Ta xác định được 1 mặt cầu duy nhất có tâm I và đi qua các điểm A, B.

Chọn B.