Câu hỏi
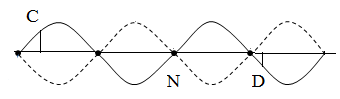
Trên một sợi dây đàn hổi đang có sóng dừng ổn định với khoảng cách giữa hai nút sóng liên tiếp là 6cm. Trên dây có những phần tử sóng dao động với tần số 5Hz và biên độ lớn nhất là 3cm. Gọi N là vị trí của một nút sóng, C và D là hai phần tử trên dây ở hai bên của N và có vị trí cân bằng cách N lần lượt là 10,5cm và 7,0cm. Tại thời điểm t1, phần tử C có li độ 1,5cm và đang hướng về vị trí cân bằng. Vào thời điểm \({t_2} = {t_1} + \frac{{85}}{{40}}s\), phần tử D có li độ là
- A 0cm
- B 1,50cm
- C – 1,50cm
- D – 0,75cm
Phương pháp giải:
Từ đề bài ta tính được bước sóng λ
Bụng sóng có biên độ 3 cm và tần số sóng là 5Hz.
Vẽ hình ta xác định được C và D nằm ở hai bó sóng khác nhau và C, D dao động ngược pha nhau.
Áp dụng công thức tính biên độ của điểm cách nút một khoảng x là:
\({A_M} = {A_b}.\left| {\sin \left( {\frac{{2\pi x}}{\lambda }} \right)} \right|\)
ta tìm được biên độ của C và D.
Sử dụng phương pháp giản đồ vecto quay để xác định li độ của C, D tại thời điểm t1 và thời điểm t2.
Lời giải chi tiết:
Từ đề bài ta tính được bước sóng:
\(\lambda = 2.6 = 12cm\)
Bụng sóng có biên độ 3 cm và tần số sóng là 5Hz.
Vẽ hình ta xác định được C và D nằm ở hai bó sóng khác nhau và C, D dao động ngược pha nhau.
Áp dụng công thức tính biên độ của điểm cách nút một khoảng x là:
\({A_M} = {A_b}.\left| {\sin \left( {\frac{{2\pi x}}{\lambda }} \right)} \right|\)
→ Biên độ của C và D là:
\(\left\{ \begin{array}{l}
{A_C} = {A_b}.\left| {\sin \left( {\frac{{2\pi x}}{\lambda }} \right)} \right| = 3.\left| {\sin \left( {\frac{{2\pi .10,5}}{{12}}} \right)} \right| = 1,5\sqrt 2 cm\\
{A_D} = {A_b}.\left| {\sin \left( {\frac{{2\pi {x_D}}}{\lambda }} \right)} \right| = 3.\left| {\sin \left( {\frac{{2\pi .7}}{{12}}} \right)} \right| = 1,5cm
\end{array} \right.\)
Ban đầu C ở vị trí có li độ 1,5 cm và đang đi về vị trí cân bằng, ta xác định được pha ban đầu của C là :
\(\sin {\varphi _{0C}} = \frac{{1,5}}{{1,5\sqrt 2 }} \Rightarrow {\varphi _{0C}} = \frac{\pi }{4}\)
Vì D ngược pha với C nên pha ban đầu của D là :
\({\varphi _{0D}} = \frac{\pi }{4} + \pi = \frac{{5\pi }}{4}\)
Vậy tại thời điểm t1 thì li độ của D là :
\({u_{D1}} = 1,5.\cos \frac{{5\pi }}{4} = - 1,5\frac{{\sqrt 2 }}{2}cm\)
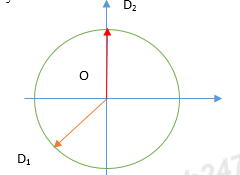
Thời điểm \({t_2} = {t_1} + \frac{{85}}{{40}}s\) thì vecto quay OD quay được góc :
\(\beta = \frac{{85}}{{40}}.2\pi f = \frac{{85}}{{40}}.2\pi .5 = 21\pi + \frac{\pi }{4}\)
Sử dụng giản đồ vecto quay:
Tại thời điểm t1vecto \(\overrightarrow {O{D_1}} \) , đến thời điểm t2ta có vecto \(\overrightarrow {O{D_2}} \)
Khi đó li độ của D là 0cm.
Chọn A