Câu hỏi
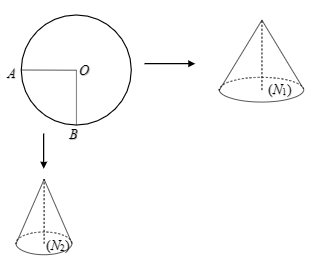
Cho một tấm nhôm hình tròn tâm O bán kính R được cắt thành hai miếng hình quạt, sau đó quấn thành hai hình nón \(\left( {{N_1}} \right)\) và \(\left( {{N_2}} \right)\). Gọi \({V_1},\,\,{V_2}\) lần lượt là thể tích của khối nón \(\left( {{N_1}} \right)\) và \(\left( {{N_2}} \right)\). Tính \(k = \dfrac{{{V_1}}}{{{V_2}}}\) biết \(AOB = {90^0}\).
- A \(k = \dfrac{{3\sqrt {105} }}{5}\)
- B \(k = 3\)
- C \(k = \dfrac{{7\sqrt {105} }}{9}\)
- D \(k = 2\)
Phương pháp giải:
- Áp dụng công thức tính diện tích hình tròn để tìm độ dài cung nhỏ và cung lớn \(AB\).
- Độ dài cung nhỏ, cung lớn \(AB\) lần lượt là chu vi đáy của hai hình nón \(\left( {{N_1}} \right)\) và \(\left( {{N_2}} \right)\).
- Tính bán kính đáy của hai hình nón \(\left( {{N_1}} \right)\) và \(\left( {{N_2}} \right)\).
- Tính chiều cao của hai hình nón \(\left( {{N_1}} \right)\) và \(\left( {{N_2}} \right)\).
- Tính lần lượt thể tích các hình nón. Hình nón có chiều cao \(h\), bán kính đáy \(r\) là \(V = \dfrac{1}{3}\pi {r^2}h\).
- Tìm tỉ số thể tích hai khối nón.
Lời giải chi tiết:
Chu vi đường tròn \(\left( {O;R} \right)\) là \(C = 2\pi R\).
Gọi \({r_1},\,\,{r_2}\) lần lượt là bán kính đáy của hình nón \(\left( {{N_1}} \right),\,\,\left( {{N_2}} \right)\).
Chu vi đáy hình nón \(\left( {{N_1}} \right)\) là: \({C_1} = \dfrac{3}{4}C = \dfrac{3}{4}.2\pi R = \dfrac{{3\pi R}}{2}\).
\( \Rightarrow 2\pi {r_1} = \dfrac{{3\pi R}}{2} \Rightarrow {r_1} = \dfrac{{3R}}{4}\)
Tương tự ta tính được \({r_2} = \dfrac{R}{4}\)
Hai hình nón đều có đường sinh \(l = R\)
Nên \({h_1} = \sqrt {{l^2} - r_1^2} = \dfrac{{\sqrt 7 }}{4}R;\)\({h_2} = \sqrt {{l^2} - r_1^2} = \dfrac{{\sqrt {15} }}{4}R.\)
\( \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\dfrac{1}{3}\pi {r_1}^2{h_1}}}{{\dfrac{1}{3}\pi {r_2}^2{h_2}}} = \dfrac{{{r_1}^2{h_1}}}{{{r_2}^2{h_2}}} = \dfrac{{\dfrac{{9{R^2}}}{{16}}.\dfrac{{\sqrt 7 }}{4}R}}{{\dfrac{{{R^2}}}{{16}}.\dfrac{{\sqrt {15} }}{4}R}} = \dfrac{{3\sqrt {105} }}{5}\)
Chọn A.







