Phương pháp giải:

Xét phương trình hoành độ giao điểm \({{x}^{3}}+\left( a+10 \right){{x}^{2}}-x+1=0\), cô lập a, đưa phương trình về dạng \(a=f\left( x \right)\), phương trình có nghiệm duy nhất \(\Leftrightarrow \) đường thẳng \(y=a\) cắt đồ thị hàm số \(y=f\left( x \right)\) tại một điểm duy nhất, lập BBT và kết luận.

Lời giải chi tiết:

Phương trình hoành độ giao điểm của \(\left( C \right)\) và \(Ox\) là \({{x}^{3}}+\left( a+10 \right){{x}^{2}}-x+1=0\)          \(\left( * \right).\)

Dễ thấy \(x=0\) không là nghiệm của phương trình \(\left( * \right).\) Khi đó \(\left( * \right)\Leftrightarrow -\,a-10=\frac{{{x}^{3}}-x+1}{{{x}^{2}}}.\)

Xét hàm số \(f\left( x \right)=\frac{{{x}^{3}}-x+1}{{{x}^{2}}}=x-\frac{1}{x}+\frac{1}{{{x}^{2}}},\) có \({f}'\left( x \right)=\frac{{{x}^{3}}+x-2}{{{x}^{3}}}=0\Leftrightarrow x=1.\)

Tính \(\underset{x\,\to \,-\,\infty }{\mathop{\lim }}\,f\left( x \right)=+\,\infty ;\,\,\underset{x\,\to \,+\,\infty }{\mathop{\lim }}\,f\left( x \right)=+\,\infty ;\,\,\underset{x\,\to \,{{0}^{\,-}}}{\mathop{\lim }}\,f\left( x \right)=-\,\infty ;\,\,\underset{x\,\to \,{{0}^{\,+}}}{\mathop{\lim }}\,f\left( x \right)=+\,\infty ;\,\,f\left( 1 \right)=1.\)

BBT:

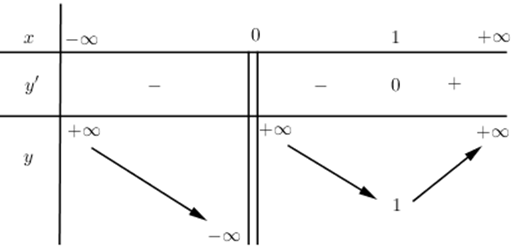
Dựa vào bảng biến thiên, ta thấy \(f\left( x \right)=-\,a-10\) có nghiệm duy nhất \(\Leftrightarrow \,\,-a-10<1\Leftrightarrow a>-\,11.\)

Kết hợp với \(a\) là số nguyên âm \(\Rightarrow \) Có 10 giá trị cần tìm.

Chọn D.