Câu hỏi
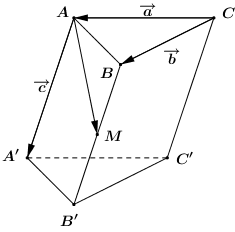
Cho hình lăng trụ \(ABC.A'B'C'\), \(M\) là trung điểm của \(BB'\). Đặt \(\overrightarrow {CA} = \overrightarrow a ,\,\,\overrightarrow {CB} = \overrightarrow b ,\,\,\overrightarrow {AA'} = \overrightarrow c \). Khẳng định nào sau đây đúng ?
- A \(\overrightarrow {AM} = \overrightarrow b + \overrightarrow c - \dfrac{1}{2}\overrightarrow a .\)
- B \(\overrightarrow {AM} = \overrightarrow a - \overrightarrow c - \dfrac{1}{2}\overrightarrow b .\)
- C \(\overrightarrow {AM} = \overrightarrow a + \overrightarrow c - \dfrac{1}{2}\overrightarrow b .\)
- D \(\overrightarrow {AM} = \overrightarrow b - \overrightarrow a + \dfrac{1}{2}\overrightarrow c .\)
Phương pháp giải:
- Sử dụng công thức trung điểm: Cho đoạn thẳng \(AB\), \(I\) là trung điểm của \(AB\). Với mọi điểm \(M\) ta có \(\overrightarrow {MI} = \dfrac{1}{2}\left( {\overrightarrow {MA} + \overrightarrow {MB} } \right)\).
- Sử dụng công thức ba điểm: \(\overrightarrow {AB} = \overrightarrow {AC} + \overrightarrow {CB} \).
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}\overrightarrow {AM} = \dfrac{1}{2}\left( {\overrightarrow {AB'} + \overrightarrow {AB} } \right)\\\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}\left( {\overrightarrow {AA'} + \overrightarrow {A'C'} + \overrightarrow {C'B'} + \overrightarrow {AC} + \overrightarrow {CB} } \right)\\\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}\left( {\overrightarrow c - \overrightarrow a + \overrightarrow b - \overrightarrow a + \overrightarrow b } \right)\\\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}\left( { - 2\overrightarrow a + 2\overrightarrow b + \overrightarrow c } \right)\\\,\,\,\,\,\,\,\,\,\, = - \overrightarrow a + \overrightarrow b + \dfrac{1}{2}\overrightarrow c \end{array}\)
Chọn D.







