Phương pháp giải:

Khoảng cách giữa 2 đường thẳng chéo nhau là độ dài đoạn vuông góc chung của 2 đường thẳng đó.

Khoảng cách giữa hai đường thẳng \(d\) và \(d'\) là khoảng cách từ 1 điểm trên \(d\) đến mặt phẳng \(\left( \alpha  \right)\) đi qua \(d'\) và song song với \(d\).

Tính cách kích thước của hình hộp chữ nhật qua các khoảng cách giữa 2 đường thẳng đã cho.

Lời giải chi tiết:

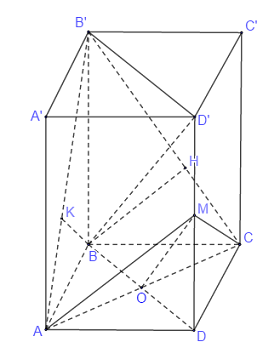
Đặt \(AA' = x;\,\,AB = y;\,\,AD = z\)

Qua \(B\),  kẻ \(BH \bot B'C\left( {H \in B'C} \right),\,\,BK \bot AB'\left( {K \in AB'} \right)\)

Ta thấy \(BH\) là đoạn vuông góc chung của 2 đường thẳng \(AB\) và \(B'C\) nên \(BH = \dfrac{{2a\sqrt 5 }}{5}\)

             \(BK\) là đoạn vuông góc chung của 2 đường thẳng \(BC\) và \(AB'\) nên \(BK = \dfrac{{2a\sqrt 5 }}{5}\)  

Do đó ta có hệ phương trình:

\(\left\{ \begin{array}{l}\dfrac{1}{{B{H^2}}} = \dfrac{1}{{B{C^2}}} + \dfrac{1}{{BB{'^2}}}\\\dfrac{1}{{B{K^2}}} = \dfrac{1}{{BB{'^2}}} + \dfrac{1}{{A{B^2}}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{{{x^2}}} + \dfrac{1}{{{z^2}}} = \dfrac{5}{{4{a^2}}}\\\dfrac{1}{{{x^2}}} + \dfrac{1}{{{y^2}}} = \dfrac{5}{{4{a^2}}}\end{array} \right.\)

Gọi \(M\) là trung điểm \(DD'\), \(O\) là giao điểm của \(AC\) và \(BD\) hay \(O\) là trung điểm \(AC\) và \(BD\).

Ta có:  \(OM\) là đường trung bình của tam giác \(BD'D\) nên \(OM//BD'\)

Do đó, \(d\left( {AC;BD'} \right) = d\left( {BD';\left( {MAC} \right)} \right) = d\left( {B;\left( {MAC} \right)} \right) = d\left( {D;\left( {MAC} \right)} \right) = \dfrac{{a\sqrt 3 }}{3}\)

Tứ diện \(D.AMC\) có 3 cạnh \(DA,DC,DM\) đôi một vuông góc nên

               \(\dfrac{1}{{{d^2}\left( {D;\left( {AMC} \right)} \right)}} = \dfrac{1}{{D{A^2}}} + \dfrac{1}{{D{C^2}}} + \dfrac{1}{{D{M^2}}}\)\( \Leftrightarrow \dfrac{1}{{{{\left( {\dfrac{x}{2}} \right)}^2}}} + \dfrac{1}{{{y^2}}} + \dfrac{1}{{{z^2}}} = \dfrac{1}{{{{\left( {\dfrac{{\sqrt 3 a}}{3}} \right)}^2}}}\)\( \Leftrightarrow \dfrac{4}{{{x^2}}} + \dfrac{1}{{{y^2}}} + \dfrac{1}{{{z^2}}} = \dfrac{3}{{{a^2}}}\) 

Do đó, ta có: \(\left\{ \begin{array}{l}\dfrac{1}{{{x^2}}} + \dfrac{1}{{{y^2}}} = \dfrac{5}{{4{a^2}}}\\\dfrac{1}{{{x^2}}} + \dfrac{1}{{{z^2}}} = \dfrac{5}{{4{a^2}}}\\\dfrac{4}{{{x^2}}} + \dfrac{1}{{{y^2}}} + \dfrac{1}{{{z^2}}} = \dfrac{3}{{{a^2}}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{{{x^2}}} = \dfrac{1}{{4{a^2}}}\\\dfrac{1}{{{y^2}}} = \dfrac{1}{{{a^2}}}\\\dfrac{1}{{{z^2}}} = \dfrac{1}{{{a^2}}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2a\\y = a\\z = a\end{array} \right.\)

Vậy thể tích của hình hộp đã cho là: \(V = xyz = 2{a^3}\).

Chọn B.