Câu hỏi
Một con lắc lò xo gồm vật nhỏ có khối lượng m = 25g và lò xo có độ cứng 100 N/m. Con lắc dao động cưỡng bức theo phương trùng với trục của lò xo dưới tác dụng của ngoại lực tuần toàn \(F = {F_0}.\cos \omega t\,\left( N \right)\). Khi ω lần lượt là 10rad/s và 15 rad/s thì biên độ dao động của vật tương ứng là A1 và A2. So sánh ta thấy:
- A \({A_1} > {A_2}\)
- B \({A_1} < {A_2}\)
- C \({A_1} = {A_2}\)
- D \({A_1} = 1,5{A_2}\)
Phương pháp giải:
+ Tần số góc của dao động riêng : \({\omega _0} = \sqrt {\dfrac{k}{m}} \)
+ Biên độ của dao động cưỡng bức càng lớn khi tần số góc của ngoại lực có giá trị càng gần giá trị của tần số góc của dao động riêng.
Lời giải chi tiết:
Tần số góc của dao động riêng :
\({\omega _0} = \sqrt {\dfrac{k}{m}} = \sqrt {\dfrac{{100}}{{0,025}}} \approx 63,25rad/s\)
Đồ thị mô tả sự phụ thuộc của biên độ vào tần số của dao động cưỡng bức :
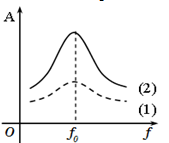
Ta có : \({\omega _1} < {\omega _2} \Rightarrow {A_1} < {A_2}\)
Chọn B.







