Phương pháp giải:

- Xác định góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.

- Sử dụng tỉ số lượng giác của các góc nhọn trong tam giác vuông và hệ thức lượng trong tam giác vuông để tính chiều cao của khối lăng trụ.

- Khối lăng trụ có chiều cao $h$, diện tích đáy $B$ có thể tích là $V = B.h$.

Lời giải chi tiết:

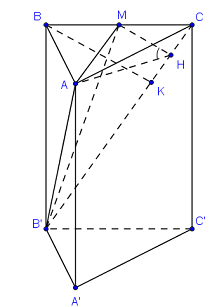
Gọi M là trung điểm của BC. Do $\Delta$ABC cân tại A nên $AM \bot BC$

Mà $AM \bot BB' \Rightarrow AM \bot \left( {BB'C} \right)$

Kẻ $MH \bot B'C,\,BK \bot B'C$$\Rightarrow \angle MHA = \left( {\left( {BB'C} \right);\left( {AB'C} \right)} \right) = {60^0}$

Tam giác ABC vuông cân tại A $\Rightarrow AM = \dfrac{{BC}}{2} = \dfrac{{2{\rm{a}}}}{2} = a$

Tam giác AMH vuông tại M, $\angle MHA = {60^0}$ $\Rightarrow MH = \dfrac{{AM}}{{\tan {{60}^0}}} = \dfrac{a}{{\sqrt 3 }}$

$\Rightarrow BK = 2.\dfrac{a}{{\sqrt 3 }} = \dfrac{{2a}}{{\sqrt 3 }}$

Tam giác BB’C vuông tại B, BK là đường cao $\Rightarrow \dfrac{1}{{B{K^2}}} = \dfrac{1}{{B{C^2}}} + \dfrac{1}{{BB{'^2}}} \Leftrightarrow \dfrac{1}{{{{\left( {\dfrac{{2a}}{{\sqrt 3 }}} \right)}^2}}} = \dfrac{1}{{{{\left( {2{\rm{a}}} \right)}^2}}} + \dfrac{1}{{BB{'^2}}}$$\Rightarrow BB' = a\sqrt 2$$\Rightarrow {V_{ABC.A'B'C'}} = {S_{ABC}}.BB' = \left( {\dfrac{1}{2}.a.2{\rm{a}}} \right).a\sqrt 2  = {a^3}\sqrt 2$.

Chọn B.