Phương pháp giải:

- Lập bảng xét dấu \(g'\left( x \right)\).

- Xác định điểm mà tại đó \(g'\left( x \right)\) đổi dấu từ âm sang dương.

Lời giải chi tiết:

Ta có : \(g'\left( x \right) = 2\left( {x - 1} \right).f'\left( {{x^2} - 2x - 4} \right).\)

\(\begin{array}{l}g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\f'\left( {{x^2} - 2x - 4} \right) = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} - 2x - 4 =  - 2\\{x^2} - 2x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} - 2x - 2 = 0\\{x^2} - 2x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 1 \pm \sqrt 3 \\x = 1 \pm \sqrt 5 \end{array} \right.\end{array}\)

Bảng xét dấu \(g'\left( x \right)\) :

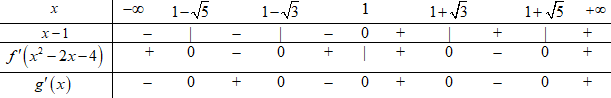
Vậy hàm số \(y = g\left( x \right) = f\left( {{x^2} - 2x - 4} \right)\) có 3 cực tiểu.

Chọn A.