Phương pháp giải:

Sử dụng công thức trọng tâm: Cho tam giác \(BCD\) có trọng tâm \(G\). Với mọi điểm \(M\) ta luôn có: \(\overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD}  = 3\overrightarrow {MG} \).

Lời giải chi tiết:

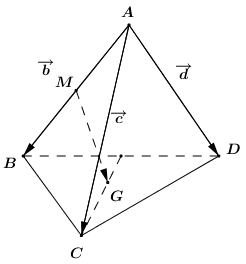
Vì \(G\) là trọng tâm tam giác \(BCD\) nên ta có:

\(\begin{array}{l}\,\,\,\,\,\,\overrightarrow {MG}  = \dfrac{1}{3}\left( {\overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD} } \right)\\ \Leftrightarrow \overrightarrow {MG}  = \dfrac{1}{3}\left( {\dfrac{1}{2}\overrightarrow {AB}  - \overrightarrow {CM}  - \overrightarrow {DM} } \right)\\ \Leftrightarrow \overrightarrow {MG}  = \dfrac{1}{6}\overrightarrow b  - \dfrac{1}{3}.\dfrac{1}{2}\left( {\overrightarrow {CA}  + \overrightarrow {CB} } \right) - \dfrac{1}{3}.\dfrac{1}{2}\left( {\overrightarrow {DA}  + \overrightarrow {DB} } \right)\\ \Leftrightarrow \overrightarrow {MG}  = \dfrac{1}{6}\overrightarrow b  - \dfrac{1}{6}\left( {\overrightarrow {CA}  + \overrightarrow {CA}  + \overrightarrow {AB} } \right) - \dfrac{1}{6}\left( {\overrightarrow {DA}  + \overrightarrow {DA}  + \overrightarrow {AB} } \right)\\ \Leftrightarrow \overrightarrow {MG}  = \dfrac{1}{6}\overrightarrow b  - \dfrac{1}{6}\left( { - 2\overrightarrow c  + \overrightarrow b } \right) - \dfrac{1}{6}\left( { - 2\overrightarrow d  + \overrightarrow b } \right)\\ \Leftrightarrow \overrightarrow {MG}  = \dfrac{1}{6}\overrightarrow b  + \dfrac{1}{3}\overrightarrow c  - \dfrac{1}{6}\overrightarrow b  + \dfrac{1}{3}\overrightarrow d  - \dfrac{1}{6}\overrightarrow b \\ \Leftrightarrow \overrightarrow {MG}  =  - \dfrac{1}{6}\overrightarrow b  + \dfrac{1}{3}\overrightarrow c  + \dfrac{1}{3}\overrightarrow d \\ \Leftrightarrow \overrightarrow {MG}  =  - \dfrac{1}{6}\left( {\overrightarrow b  - 2\overrightarrow c  - 2\overrightarrow d } \right)\end{array}\)

Vậy \(\overrightarrow {MG}  =  - \dfrac{1}{6}\left( {\overrightarrow b  - 2\overrightarrow c  - 2\overrightarrow d } \right)\).

Chọn A.