Câu hỏi
Cho hàm số bậc ba có đồ thị là đường cong hình bên dưới.
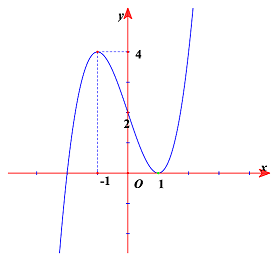
Đồ thị hàm số \(g\left( x \right) = \dfrac{{\left( {x - 1} \right)\left( {{x^2} - 1} \right)}}{{{f^2}\left( x \right) - 2f\left( x \right)}}\) có tất cả bao nhiêu đường tiệm cận đứng?
- A \(2\)
- B \(4\)
- C \(3\)
- D \(1\)
Phương pháp giải:
- Định nghĩa tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\): Nếu \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = + \infty \,\) hoặc \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = - \infty \,\) hoặc \(\mathop {\lim }\limits_{x \to {a^ - }} f(x) = + \infty \,\) hoặc \(\mathop {\lim }\limits_{x \to {a^ - }} f(x) = - \infty \,\) thì \(x = a\) là TCĐ của đồ thị hàm số.
- Tìm các nghiệm của phương trình mẫu và kết luận các đường tiệm cận đứng của đồ thị hàm số.
Lời giải chi tiết:
Ta có: \(g\left( x \right) = \dfrac{{\left( {x - 1} \right)\left( {{x^2} - 1} \right)}}{{{f^2}\left( x \right) - 2f\left( x \right)}} = \dfrac{{{{\left( {x - 1} \right)}^2}\left( {x + 1} \right)}}{{f\left( x \right)\left( {f\left( x \right) - 2} \right)}}.\)
Xét phương trình tử số: \({\left( {x - 1} \right)^2}\left( {x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\) (\(x = 1\) là nghiệm bội 2, \(x = - 1\) là nghiệm đơn).
Xét phương trình mẫu số: \(f\left( x \right)\left[ {f\left( x \right) - 2} \right] = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 0\\f\left( x \right) = 2\end{array} \right.\).
+ Xét phương trình \(f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 1\end{array} \right.\).
Dựa vào đồ thị hàm số ta thấy \(x = - 2\) là nghiệm đơn, \(x = 1\) là nghiệm bội 2.
+ Xét phương trình \(f\left( x \right) = 2 \Leftrightarrow \left[ \begin{array}{l}x = {x_1}\,\,\left( { - 2 < {x_1} < - 1} \right)\\x = 0\\x = {x_2}\,\,\left( {1 < {x_2} < 2} \right)\end{array} \right.\) (Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 2\) song song với trục hoành).
Dựa vào đồ thị hàm số ta thấy tất cả các nghiệm \(x = {x_1}\), \(x = 0\), \(x = {x_2}\) đều là nghiệm đơn.
Vậy đồ thị hàm số có 4 đường tiệm cận đứng là: \(x = - 2\), \(x = {x_1}\),\(x = {x_2}\),\(x = 0\).
Chọn: B.







