Cho tam giác ABC. Điểm M thỏa mãn là

Câu hỏi

Cho tam giác ABC. Điểm M thỏa mãn 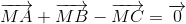$\overrightarrow {MA} + \overrightarrow {MB} - \overrightarrow {MC} = \overrightarrow 0$ là

A Trọng tâm của tam giác ABC.
B Đỉnh thứ tư của hình bình hành nhận AC và BC làm hai cạnh.
C Đỉnh thứ tư của hình bình hành nhận AC và AB làm hai cạnh.
D Đỉnh thứ tư của hình bình hành nhận AB và BC làm hai cạnh.

Lời giải chi tiết:

Ta có: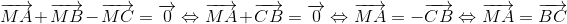 $\overrightarrow {MA} + \overrightarrow {MB} - \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MA} + \overrightarrow {CB} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MA} = - \overrightarrow {CB} \Leftrightarrow \overrightarrow {MA} = \overrightarrow {BC}$

Khi đó M là đỉnh thứ 4 của 1 hình bình hành thỏa mãn MA // BC và MA = BC.

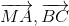$\overrightarrow {MA} ,\overrightarrow {BC}$ cùng hướng.Từ đó ta có hình vẽ sau

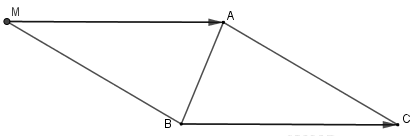
Chọn B.

Câu hỏi trước Câu hỏi tiếp theo

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

TẢI APP ĐỂ XEM OFFLINE