Phương pháp giải:

Cách 1:

+) Tìm GTLN và GTNN của hàm số \(y = f\left( x \right)\) trên \(\left[ {a;\;b} \right]\) bằng cách:

+) Giải phương trình \(y' = 0\) tìm các nghiệm \({x_i}.\)

+) Tính các giá trị \(f\left( a \right),\;f\left( b \right),\;\;f\left( {{x_i}} \right)\;\;\left( {{x_i} \in \left[ {a;\;b} \right]} \right).\)  Khi đó:

\(\mathop {\min }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \min \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\},\;\;\mathop {\max }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \max \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\}.\) 

Cách 2: Sử dụng chức năng MODE 7 để tìm GTLN, GTNN của hàm số trên \(\left[ {a;\;b} \right].\)

Lời giải chi tiết:

Xét hàm số \(y = x - \sqrt {x - 2} \) trên \(\left[ {2;\,\,6} \right]\)

Hàm số \(y = x - \sqrt {x - 2}  \Rightarrow y' = 1 - \frac{1}{{2\sqrt {x - 2} }}\)

\(\begin{array}{l} \Rightarrow y' = 0 \Leftrightarrow 2\sqrt {x - 2}  = 1\\ \Leftrightarrow 4x - 8 = 1 \Leftrightarrow x = \frac{9}{4}\,\, \in \left[ {2;\,\,6} \right]\end{array}\)

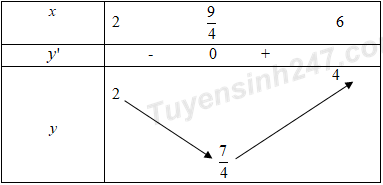
Bảng biến thiên:

Dựa vào bảng biến thiên ta có: \(M = 4;\,\,m = \frac{7}{4}\)

\( \Rightarrow M - m = \frac{9}{4}.\)

Chọn C.