Câu hỏi
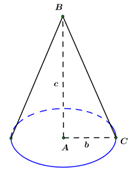
Cho tam giác ABC vuông tại \(A,\,\,AB = c,\,\,AC = b.\) Quay tam giác \(ABC\) xung quanh đường thẳng chứa cạnh \(AB\) ta được một hình nón có thể tích bằng :
- A \(\frac{1}{3}\pi b{c^2}.\)
- B \(\frac{1}{3}b{c^2}.\)
- C \(\frac{1}{3}{b^2}c.\)
- D \(\frac{1}{3}\pi {b^2}c.\)
Phương pháp giải:
Thể tích khối nón có bán kính đáy \(R\) và chiều cao \(h:\;\;\;V = \frac{1}{3}\pi {R^2}h.\)
Lời giải chi tiết:
Khi quay \(\Delta ABC\) vuông tại \(A\) quanh đường thẳng chứa cạnh \(AB\) ta được hình nón có đường cao \(h = AB = c,\) bán kính đáy \(r = AC = b.\) Khi đó thể tích khối nón được tạo thành là: \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {b^2}c.\)
Chọn D.
Câu hỏi trước
