Câu hỏi
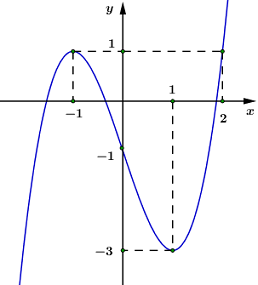
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên. Gọi \(g\left( x \right) = f\left( x \right) - \dfrac{1}{3}{x^3} + \dfrac{1}{2}{x^2} + x - 2019.\) Biết \(g\left( { - 1} \right) + g\left( 1 \right) > g\left( 0 \right) + g\left( 2 \right).\) Với \(x \in \left[ { - 1;\,\,2} \right]\) thì \(g\left( x \right)\) đạt giá trị nhỏ nhất bằng:
- A \(g\left( 2 \right)\)
- B \(g\left( 1 \right)\)
- C \(g\left( { - 1} \right)\)
- D \(g\left( 0 \right)\)
Lời giải chi tiết:
Ta có: \(g'\left( x \right) = f'\left( x \right) - {x^2} + x + 1\).
\(g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = {x^2} - x - 1\).
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f'\left( x \right)\) và \(y = {x^2} - x - 1\).
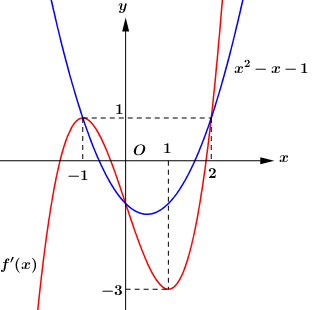
Dựa vào đồ thị hàm số ta thấy \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 0\\x = 2\end{array} \right.\).
BBT:
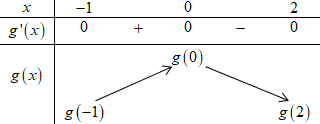
So sánh \(g\left( { - 1} \right)\) và \(g\left( 2 \right)\).
Ta có \(g\left( { - 1} \right) + g\left( 1 \right) > g\left( 0 \right) + g\left( 2 \right)\)\( \Leftrightarrow g\left( { - 1} \right) - g\left( 2 \right) > g\left( 0 \right) - g\left( 1 \right)\).
Dựa vào BBT ta thấy hàm số nghịch biến trên \(\left( {0;2} \right)\) nên \(g\left( 0 \right) > g\left( 1 \right) \Rightarrow g\left( 0 \right) - g\left( 1 \right) > 0\).
Suy ra \(g\left( { - 1} \right) - g\left( 2 \right) > 0 \Leftrightarrow g\left( { - 1} \right) > g\left( 2 \right)\).
Vậy \(\mathop {\min }\limits_{\left[ { - 1;2} \right]} g\left( x \right) = g\left( 2 \right)\).
Chọn A.







