Lời giải chi tiết:

Ta có:

\(\begin{array}{l}f'\left( x \right) = \dfrac{{x\cos x - \sin x}}{{{x^2}}},\forall x \ne 0.\\f'\left( x \right) = 0 \Leftrightarrow x\cos x = \sin x \Leftrightarrow x = \tan x.\end{array}\)

Từ đây xét đồ thị hàm số \(y = \tan x\) và \(y = x\).

Ta có đồ thị hàm số như sau:

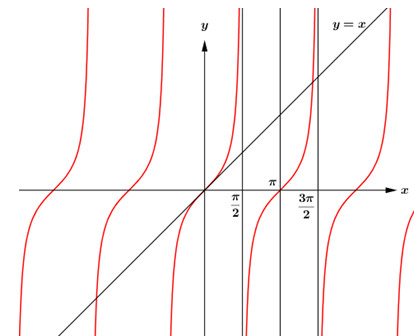
Trên mỗi khoảng: \(\left( {k\pi ;\dfrac{\pi }{2} + k\pi } \right)\,\,\left( {k \in \mathbb{Z}} \right)\) thì phương trình \(f'\left( x \right) = 0\) có 1 nghiệm, và rõ ràng qua nghiệm này \(f'\left( x \right)\) đổi dấu, lại xét trên khoảng \(\left( {0;\,\,100\pi } \right)\) nên ta có:

\(\left\{ \begin{array}{l}0 < k\pi \\\dfrac{\pi }{2} + k\pi  < 100\pi \end{array} \right. \Rightarrow 0 < k < 99,5\). Mà \(k \in \mathbb{Z} \Rightarrow k \in \left\{ {1;2;3;...;99} \right\}\).

Vậy có 99 giá trị \(k\) thỏa mãn.

Chọn C.