Phương pháp giải:

- Tính bán kính đường tròn nội tiếp đáy, sử dụng công thức \(r = \dfrac{S}{p}\) trong đó \(S,\,\,p\) lần lượt là diện tích và nửa chu vi của tam giác.

- Sử dụng định lí Pytago tính chiều cao của hình tứ diện.

- Diện tích xung quanh hình trụ có chiều cao \(h\), bán kính đáy \(r\) là \({S_{xq}} = 2\pi rh\).

Lời giải chi tiết:

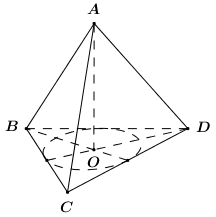
Tam giác \(BCD\) đều cạnh \(a\) nên \({S_{\Delta BCD}} = \dfrac{{{4^2}\sqrt 3 }}{4} = 4\sqrt 3 \).

Gọi \(p\) là nửa chu vi tam giác \(BCD\) ta có \(p = \dfrac{{3.4}}{2} = 6\).

Khi đó bán kính đường tròn nội tiếp tam giác \(BCD\) là \(r = \dfrac{S}{p} = \dfrac{{4\sqrt 3 }}{6} = \dfrac{{2\sqrt 3 }}{3}\), đây cũng chính là bán kính đáy của hình trụ.

Gọi \(O\) là trọng tâm tam giác \(BCD\) ta có \(AO \bot \left( {BCD} \right)\).

Xét tam giác vuông \(SOB\) có; \(BO = \dfrac{2}{3}.\dfrac{{4\sqrt 3 }}{2} = \dfrac{{4\sqrt 3 }}{3}\), \(AB = 4\).

\( \Rightarrow AO = \sqrt {A{B^2} - B{O^2}}  = \sqrt {{4^2} - {{\left( {\dfrac{{4\sqrt 3 }}{3}} \right)}^2}}  = \dfrac{{4\sqrt 6 }}{3}\), đây cũng chính là chiều cao của hình trụ.

Vậy diện tích xung quanh hình trụ là \({S_{xq}} = 2\pi .\dfrac{{2\sqrt 3 }}{3}.\dfrac{{4\sqrt 6 }}{3} = \dfrac{{16\sqrt 2 \pi }}{3}\).

Chọn A.