Câu hỏi
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(\left| {f\left( x \right)} \right| = 2\) là:
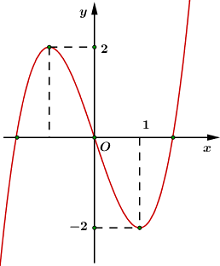
- A \(6\)
- B \(4\)
- C \(3\)
- D \(2\)
Phương pháp giải:
Từ đồ thị hàm số \(y = f\left( x \right),\) suy ra đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) bằng cách giữ lại phần đồ thị phía trên trục \(Ox,\) lấy đối xứng phần đồ thị phía dưới trục \(Ox\) lên phía trên trục \(Ox.\)
Số nghiệm của phương trình \(\left| {f\left( x \right)} \right| = 2\) là số giao điểm của đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) và đường thẳng \(y = 2.\)
Dựa vào đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) để tìm số giao điểm của hai đồ thị hàm số.
Lời giải chi tiết:
Số nghiệm của phương trình \(\left| {f\left( x \right)} \right| = 2\) là số giao điểm của đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) và đường thẳng \(y = 2.\)
Ta có đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) như sau:
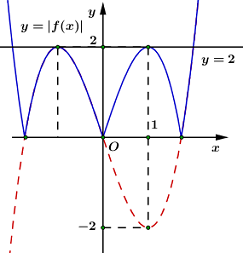
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = 2\) cắt đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) tại \(4\) điểm phân biệt.
Chọn B.







