Câu hỏi
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
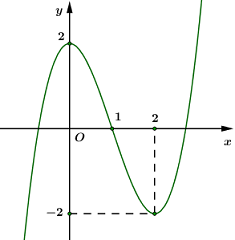
- A \(y = - {x^3} + 3{x^2} + 2\)
- B \(y = {x^3} - 3x + 2\)
- C \(y = - {x^4} + 2{x^2} - 2\)
- D \(y = {x^3} - 3{x^2} + 2\)
Phương pháp giải:
Dựa vào đồ thị hàm số nhận xét tính đơn điệu của hàm số và các điểm mà đồ thị hàm số đi qua để từ đó chọn hàm số đúng.
Lời giải chi tiết:
Ta thấy đồ thị hàm số có nét cuối đi lên nên \(a > 0 \Rightarrow \) loại đáp án A và C.
Hàm số có hai điểm cực trị là \(x = 0\) và \(x = 2.\)
+) Xét đáp án B:\(y = {x^3} - 3x + 2\) có \(y' = 3{x^2} - 3\)
\( \Rightarrow y' = 0 \Leftrightarrow 3{x^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
\( \Rightarrow \) Hàm số có hai điểm cực trị là \(x = - 1\) và \(x = 1.\)
\( \Rightarrow \) loại đáp án B.
Chọn D.







