Phương pháp giải:

Phương pháp tìm GTLN, GTNN của hàm số \(y = f\left( x \right)\) trên \(\left[ {a;b} \right]\).

- Giải phương trình \(f'\left( x \right) = 0\) suy ra các nghiệm \({x_i} \in \left[ {a;b} \right]\).

- Tính \(f\left( a \right),\,\,f\left( b \right),\,\,f\left( {{x_i}} \right)\).

- Kết luận: \(\mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right) = \max \left\{ {f\left( a \right),\,\,f\left( b \right),\,\,f\left( {{x_i}} \right)} \right\}\), \(\mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right) = \min \left\{ {f\left( a \right),\,\,f\left( b \right),\,\,f\left( {{x_i}} \right)} \right\}\).

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).

Ta có: \(f'\left( x \right) =  - 1 + \dfrac{1}{{{x^2}}} = \dfrac{{1 - {x^2}}}{{{x^2}}}\).

\(f'\left( x \right) = 0 \Leftrightarrow 1 - {x^2} = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \left( {0;4} \right)\\x =  - 1 \notin \left( {0;4} \right)\end{array} \right.\).

BBT:

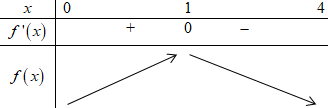
Dựa vào BBT ta có: \(\mathop {\max }\limits_{\left( {0;4} \right)} f\left( x \right) = f\left( 1 \right)\)\( \Rightarrow {x_0} = 1\).

Vậy \(P = {x_0} + 2018 = 2019\).

Chọn D.